Warpspeed confidence -- what is credible?

The Very Basics

If you have some background in statistics the next section may be a little boring for you but bear with me I promise an opportunity to delve more deeply later and revisit more complex issues like the differences between frequentist and bayesian methods later. I’ve explored this topic before but there’s plenty of new stuff below. Let’s just get the basics under our belts.

If you’ve ever taken an introductory course in probability and statistics you’ve likely been exposed to the statistician’s love of coin flips. This is another instance where at it’s simplest comparing our vaccine trials to coin flips can be instructive. Although overall the study is a randomized controlled trial (actually several of them) on a very large scale in many ways our understanding of these first 53 cases can be modeled as a set of coin flips. For each of the 53 people who are confirmed to have contracted covid-19 they either got the vaccine or a placebo (heads or tails).

R let’s us quickly get a sense of what the probability is that of the 53 people in the trial who contracted covid-19 what if only the minimum of 5 were given the actual vaccine and not the placebo? For those of you who don’t like scientific notation that’s thirty-one billion, eight hundred fifty-nine million, nine hundred thousand probability against you doing that randomly flipping coins.

got_covid <- 53
vaccinated_got_covid <- 5
placebo_got_covid <- 53 - vaccinated_got_covid
dbinom(vaccinated_got_covid, got_covid, .5)

## [1] 3.18599e-10

vaccinated_got_covid <- 19
placebo_got_covid <- 53 - vaccinated_got_covid
dbinom(vaccinated_got_covid, got_covid, .5)

## [1] 0.01321525

Even if 19 people who received the true vaccine got covid the probability is still less than 2% that the vaccine versus placebo doesn’t matter that it’s a 50/50 chance.

Let’s talk about effectiveness. We want our vaccine to be at least 50% effective. We can operationalize that most simply by \[\frac{placebo~cases - vaccinated~cases}{placebo~cases}\] So for our current example where 19 of the 53 cases had received the vaccine our effectiveness is \[\frac{placebo~cases - vaccinated~cases}{placebo~cases} = (34-19)/34 = 0.4411765\] which is very close to what we need. Let’s display it graphically for the range between 5 and 26 vaccinated cases and dispense with one other pesky issue. So far we have been ignoring the fact that there aren’t 53 people involved in the trial, there are 30,000. We don’t really want to lose sight of this even though it makes very little difference to our math in most cases. Let’s calculate effectiveness both with and without 30,000 in the denominator and even track rounding error in our little tibble.

library(dplyr)
library(ggplot2)
library(kableExtra)
theme_set(theme_bw())

effectiveness <-
   tibble::tibble(vaccinated = 5:26) %>%
   mutate(placebo = 53 - vaccinated,
          effectiveness = (placebo - vaccinated) / placebo * 100,
          placeborate = placebo / (15000 - placebo),
          vaccinatedrate = vaccinated / (15000 - vaccinated),
          pctratedifference = (placeborate - vaccinatedrate) / placeborate * 100,
          rounding = effectiveness - pctratedifference)

effectiveness %>%
  kbl(digits = c(0,0,2,4,4,2,2),
      caption = "Effectiveness as a function of positive COVID cases") %>%
  kable_minimal(full_width = FALSE, 
      position = "left") %>%
  add_header_above(c("Cases (53)" = 2, " " = 1, "Infection Rate" = 2, "% difference in rate" = 1, " " = 1))

Table 1: Effectiveness as a function of positive COVID cases

Cases (53)			Infection Rate		% difference in rate
vaccinated	placebo	effectiveness	placeborate	vaccinatedrate	pctratedifference	rounding
5	48	89.58	0.0032	0.0003	89.61	-0.03
6	47	87.23	0.0031	0.0004	87.27	-0.03
7	46	84.78	0.0031	0.0005	84.82	-0.04
8	45	82.22	0.0030	0.0005	82.27	-0.04
9	44	79.55	0.0029	0.0006	79.59	-0.05
10	43	76.74	0.0029	0.0007	76.80	-0.05
11	42	73.81	0.0028	0.0007	73.86	-0.05
12	41	70.73	0.0027	0.0008	70.79	-0.06
13	40	67.50	0.0027	0.0009	67.56	-0.06
14	39	64.10	0.0026	0.0009	64.16	-0.06
15	38	60.53	0.0025	0.0010	60.59	-0.06
16	37	56.76	0.0025	0.0011	56.82	-0.06
17	36	52.78	0.0024	0.0011	52.84	-0.06
18	35	48.57	0.0023	0.0012	48.63	-0.06
19	34	44.12	0.0023	0.0013	44.17	-0.06
20	33	39.39	0.0022	0.0013	39.45	-0.05
21	32	34.38	0.0021	0.0014	34.42	-0.05
22	31	29.03	0.0021	0.0015	29.07	-0.04
23	30	23.33	0.0020	0.0015	23.37	-0.04
24	29	17.24	0.0019	0.0016	17.27	-0.03
25	28	10.71	0.0019	0.0017	10.73	-0.02
26	27	3.70	0.0018	0.0017	3.71	-0.01

effectiveness %>%
   ggplot(aes(x = vaccinated)) +
   geom_line(aes(y = effectiveness)) +
   geom_line(aes(y = pctratedifference), color = "green") +
   geom_hline(aes(yintercept = 50)) +
   scale_y_continuous(labels = scales::label_percent(scale = 1),
                      breaks = seq.int(0, 100, 10)) +
   scale_x_continuous(breaks = seq.int(2, 26, 2)) +
   xlab("Number of positive COVID-19 outcomes among those who received the vaccine") +
   ylab("Effectiveness as a percentage") +
   ggtitle("Vaccine effectiveness as a function of outcomes (53 total cases)")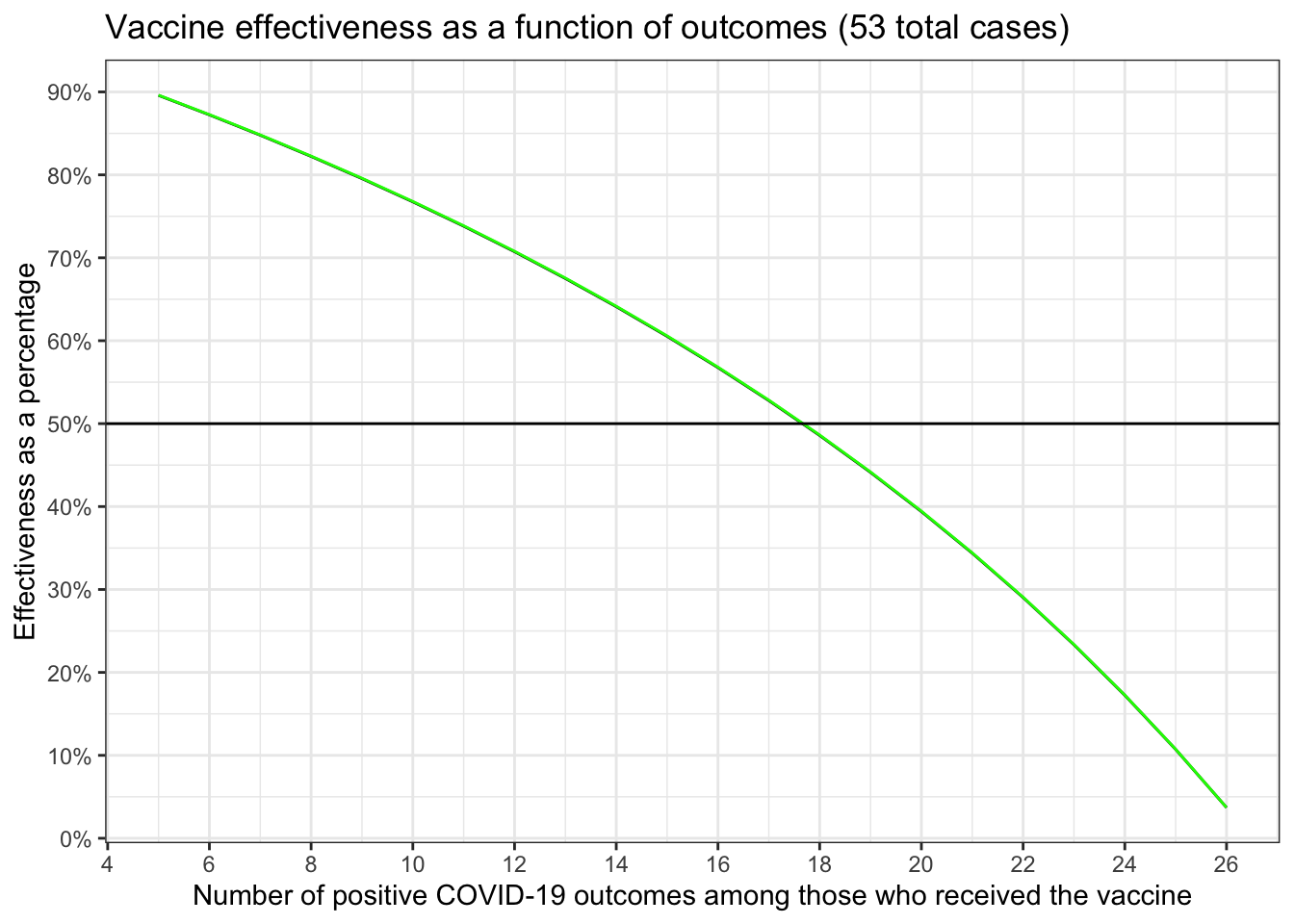

mean(effectiveness$rounding) # that's .04% not 4.0%

## [1] -0.04559179

So in the best possible scenario (remember we require that at least 5 people who got the vaccine contract COVID before we can run the numbers) our effectiveness is ~90%. We need the number of people who received the vaccine and still contracted COVID to be 17 or less.

Testing our confidence as a frequentist

Now we know what we have to do to convince ourselves about effectiveness let’s address what we can do to be confident that our results are not a fluke. We know that low probability events occur. I don’t want to repeat myself so if you want a little background on frequentist methodology please see this earlier post. If you want one of many cautionary tails about the limits of NHST then please see this post.

Having said all that, frequentist methods are certainly the most prevalent and likely to be applied to the warpspeed data so let’s see what we come up with. Let’s start with the simplest possible test we could use. Let’s build a simple matrix (table) of our results and call it dat. We’ll assume the 30,000 participants are equally divided between receiving the vaccine and the placebo. We’ll pretend 19 folks who got the real vaccine later developed COVID and 34 did not. We’ll grab just the first column dat[,1] and put that in an object called covid_gof. Our hypothesis is that the vaccine matters that it helps prevent being infected. In NHST terms our null hypothesis is that there is no difference in the number of people who will get infected. In essence it might as well be a coin toss, 50/50, equal numbers of people will get infected whether they received the vaccine or the placebo. We can use the \(\chi^2\) goodness of fit test. For clarity we’ll remove the continuity correction and overtly specify 50/50 odds. Since the default chisq.test test results are very terse we’ll use lsr::goodnessOfFitTest on the same data (expressed as vector that is a factor) to make it clear what we’re doing.

dat <- matrix(c(34, 15000 - 34, 19, 15000 - 19),
              nrow = 2,
              byrow = TRUE)
rownames(dat) <- c("Placebo", "Vaccine")
colnames(dat) <- c("COVID", "No COVID")
dat

##         COVID No COVID
## Placebo    34    14966
## Vaccine    19    14981

covid_gof <- dat[,1]

chisq.test(covid_gof, 
           correct = FALSE, 
           p = c(.5, .5))

## 
##  Chi-squared test for given probabilities
## 
## data:  covid_gof
## X-squared = 4.2453, df = 1, p-value = 0.03936

outcomes <- factor(c(rep("Vaccine", 19), rep("Placebo", 34)))
lsr::goodnessOfFitTest(outcomes)

## 
##      Chi-square test against specified probabilities
## 
## Data variable:   outcomes 
## 
## Hypotheses: 
##    null:        true probabilities are as specified
##    alternative: true probabilities differ from those specified
## 
## Descriptives: 
##         observed freq. expected freq. specified prob.
## Placebo             34           26.5             0.5
## Vaccine             19           26.5             0.5
## 
## Test results: 
##    X-squared statistic:  4.245 
##    degrees of freedom:  1 
##    p-value:  0.039

Either way \(\chi^2\) = 4.245283 and p = 0.0393595. Therefore we reject the null and can have some “confidence” that our results aren’t simply a fluke.

That seems a little too simple and seems to ignore the fact that we actually have data for not 53 people but 30,000 people. So let’s make things more complex. There are actually many variants of a \(\chi^2\) test. Instead of goodness of fit let’s use \(\chi^2\) test of independence or association using all four cells of our little matrix. Here our null hypothesis is that our variables are independent of one another, that whether you get COVID has no association to whether you received the vaccine or the placebo. A subtle distinction perhaps but worth it if for no other reason than to exploit the additional data. To make it even more fun there are numerous functions in r to run the test. From base r, where there are at least two variants chisq.test and prop.test to specialized packages like epiR that focus on epidemiology.

Notice that they all express the same basic notions \(\chi^2\) = 4.2527963 and p = 0.0391858, even though they present an array of additional information.

chisq.test(dat, correct = FALSE)

## 
##  Pearson's Chi-squared test
## 
## data:  dat
## X-squared = 4.2528, df = 1, p-value = 0.03919

prop.test(dat, correct = FALSE)

## 
##  2-sample test for equality of proportions without continuity
##  correction
## 
## data:  dat
## X-squared = 4.2528, df = 1, p-value = 0.03919
## alternative hypothesis: two.sided
## 95 percent confidence interval:
##  0.0000496578 0.0019503422
## sample estimates:
##      prop 1      prop 2 
## 0.002266667 0.001266667

epiR::epi.2by2(dat = as.table(dat), method = "cross.sectional",
         conf.level = 0.95, units = 1, outcome = "as.columns")

##              Outcome +    Outcome -      Total        Prevalence *        Odds
## Exposed +           34        14966      15000             0.00227     0.00227
## Exposed -           19        14981      15000             0.00127     0.00127
## Total               53        29947      30000             0.00177     0.00177
## 
## Point estimates and 95% CIs:
## -------------------------------------------------------------------
## Prevalence ratio                             1.79 (1.02, 3.14)
## Odds ratio                                   1.79 (1.02, 3.14)
## Attrib prevalence *                          0.00 (0.00, 0.00)
## Attrib prevalence in population *            0.00 (-0.00, 0.00)
## Attrib fraction in exposed (%)              44.12 (2.08, 68.11)
## Attrib fraction in population (%)           28.30 (-2.75, 49.97)
## -------------------------------------------------------------------
##  Test that OR = 1: chi2(1) = 4.253 Pr>chi2 = 0.04
##  Wald confidence limits
##  CI: confidence interval
##  * Outcomes per population unit

Notice that epiR::epi.2by2 provides confirmation of several important pieces of data we generated earlier in our very first table results. If you consult the row for 19 & 34, prevalence matches 0.00227 & 0.00127 the columns labeled “infection rate” and “Attrib fraction in exposed (%) = 44.12” matches our “effectiveness” column.

Credible? Incredible? A bayesian approach to how confident we are

The “problem” with a frequentist’s approach is that the “testing” framework is rather contorted and you really can’t make the statements that you want to make. We want to use the language of probability theory to say things like “there is an 90% chance that the vaccine is effective, which of course means there’s a 10% chance that it doesn’t”. As I have written before and many others have written elsewhere a “p value” and a “confidence interval” don’t give you that capability. Don’t get me wrong, the approach can be useful, is still the most frequent and dominant approach, but I don’t find it the best approach.

So let’s approach our warpspeed data using several different tools and allow ourselves the joy (okay I know that sounds geeky) to make probabilistic statements about what the data tell us. The rest of this post will be all about using bayesian tools.

Since I’m always a fan of making use of existing packages and code that do what I want them to do I did some exploration looking to see what was available. One of the first things I stumbled upon was a very nice function bayes.prop.test contained in a package called bayesian_first_aid, sadly but not surprisingly there was no CRAN version and development appears to have stopped circa 2015. Not surprising because there has been a lot more code published for Bayesian methods since then and I know how much work it takes to keep up a package. There are others I’ll demonstrate a little later but the appeal of this function is it’s simplicity. It’s a great place to start the code was easy to follow so I just grabbed the framework and updated it for my own needs. The Github code is here.

It’s fiendishly easy to set-up and run. We’ll go back to our original dat object and divide it up by column. Column 1 those who got COVID by condition “Placebo” and “Vaccine” and column 2 those who didn’t. To keep this from being tl;dr I’m not going to go into too much detail on jags and runjags. If you need a good tutorial consult a reference like DBDA. I’ll only highlight the key points. For purposes of this post I’m going to use a flat, uninformed prior in all cases (this time the specific line is theta[i] ~ dbeta(1, 1)). One of the nice aspects of bayesian inference is you can express your prior thinking/knowledge mathematically, then let the data inform your thinking. Given the vaccine has already been involved in significant phase I and II trials it wouldn’t be unusual to have a prior that expressed at least a little confidence that it had some effect. But we’ll pretend we know nothing and that any outcome is equally likely. We’re back to flipping coins again.

We’re going to explore the probabilities that the percentage of positive cases among those who received the vaccine is the same as the percentage of positive cases among those who received the vaccine. The model is constructed so that we could conceivably have more than two possibilities (e.g. easy to extend to a case where we had two different vaccines + a placebo or two different doses of the same vaccine plus placebo). That is very likely to be modeled later or when more data are in. We’ll “monitor” results for the infection rate placebo and vaccine (theta[1] and theta[2] respectively). As well as the raw predictions of how many people (x_pred[1] and x_pred[2]), not strictly necessary but fun to watch.

This is a simple model with just four data elements we need to enter but we’ll still run it in 4 chains spread across 4 cores. If you’re following along I’m suppressing some messages about not choosing different random seeds per chain (run_jags will pick some), and that we used the same initial value for all chains (also not a worry). You should also run plot(my_results) to check the diagnostics for convergence and auto-correlation. I did, they’re fine but to save screen real estate I won’t include them.

# Setting up the data
dat

##         COVID No COVID
## Placebo    34    14966
## Vaccine    19    14981

got_covid <- dat[,1] 
not_covid <- dat[,2] 
got_covid

## Placebo Vaccine 
##      34      19

not_covid

## Placebo Vaccine 
##   14966   14981

# The model string written in the JAGS language
model_string <- "model {
  for(i in 1:length(got_covid)) {
    got_covid[i] ~ dbinom(theta[i], not_covid[i])
    theta[i] ~ dbeta(1, 1)
    x_pred[i] ~ dbinom(theta[i], not_covid[i])
  }
}"

my_results <- runjags::run.jags(model_string,
                  sample = 10000,
                  n.chains=4,
                  method="parallel",
                  monitor = c("theta", "x_pred"),
                  data = list(got_covid = got_covid, 
                              not_covid = not_covid))

## Calling 4 simulations using the parallel method...
## Following the progress of chain 1 (the program will wait for all chains
## to finish before continuing):
## Welcome to JAGS 4.3.0 on Wed Nov  4 15:53:41 2020
## JAGS is free software and comes with ABSOLUTELY NO WARRANTY
## Loading module: basemod: ok
## Loading module: bugs: ok
## . . Reading data file data.txt
## . Compiling model graph
##    Resolving undeclared variables
##    Allocating nodes
## Graph information:
##    Observed stochastic nodes: 2
##    Unobserved stochastic nodes: 4
##    Total graph size: 9
## . Reading parameter file inits1.txt
## . Initializing model
## . Adapting 1000
## -------------------------------------------------| 1000
## ++++++++++++++++++++++++++++++++++++++++++++++++++ 100%
## Adaptation successful
## . Updating 4000
## -------------------------------------------------| 4000
## ************************************************** 100%
## . . . Updating 10000
## -------------------------------------------------| 10000
## ************************************************** 100%
## . . . . Updating 0
## . Deleting model
## . 
## All chains have finished
## Simulation complete.  Reading coda files...
## Coda files loaded successfully
## Calculating summary statistics...
## Calculating the Gelman-Rubin statistic for 4 variables....
## Finished running the simulation

my_results

## 
## JAGS model summary statistics from 40000 samples (chains = 4; adapt+burnin = 5000):
##                                                                              
##              Lower95    Median   Upper95      Mean         SD Mode      MCerr
## theta[1]   0.0015968 0.0023139 0.0031255 0.0023355  0.0003931   -- 2.4955e-06
## theta[2]  0.00078245 0.0013134 0.0019311 0.0013362 0.00029839   -- 1.9488e-06
## x_pred[1]         18        34        50    34.939     8.2756   33   0.047637
## x_pred[2]          8        19        32    19.991     6.3011   19   0.035686
##                                          
##           MC%ofSD SSeff      AC.10   psrf
## theta[1]      0.6 24813 -0.0078862 1.0002
## theta[2]      0.7 23445  0.0014997 1.0002
## x_pred[1]     0.6 30180 -0.0048487 1.0003
## x_pred[2]     0.6 31177  0.0088355 1.0001
## 
## Total time taken: 1.3 seconds

# plot(my_results) ## diagnostics were checked.

Okay that all looks quite complex, what do we do now? Let’s first investigate the things we care most about. Remember theta[1] & theta[2] represent our infection rates theta[1] = 0.0023355 is our rate among those who got the placebo and theta[2] = 0.0013362 is our rate among those who got the vaccine. Those are the mean values and the medians are similar. The x_pred values are estimates of the case counts.

We can use tidybayes::tidy_draws to extract the results of our 40,000 chains and pipe it through select to get the columns we want with the names we’d like. As much as I like Greek \(\theta\) gets old after awhile. At the same time we can compute via a mutate statement what we really want to know which is the % difference in infection rates which we’ll put in a column called diff_rate.

Now when we pass this cleaned up data to bayestestR::describe_posterior(results1) we get back a table that is a little easier to read. Focus on just the line for diff_rate.

results1 <- 
   tidybayes::tidy_draws(my_results) %>%
   select(placebo_rate = `theta[1]`,
          vaccine_rate = `theta[2]`,
          placebo_cases = `x_pred[1]`,
          vaccine_cases = `x_pred[2]`) %>%
   mutate(diff_rate = (placebo_rate - vaccine_rate) / placebo_rate * 100)

glimpse(results1)

## Rows: 40,000
## Columns: 5
## $ placebo_rate  <dbl> 0.00223850, 0.00266489, 0.00317073, 0.00272058, 0.00243…
## $ vaccine_rate  <dbl> 0.000943283, 0.001122100, 0.001294810, 0.001245260, 0.0…
## $ placebo_cases <dbl> 35, 38, 34, 36, 32, 34, 35, 42, 33, 29, 30, 39, 37, 35,…
## $ vaccine_cases <dbl> 14, 17, 19, 16, 29, 17, 21, 19, 15, 20, 14, 27, 10, 19,…
## $ diff_rate     <dbl> 57.86093, 57.89320, 59.16366, 54.22814, 39.60447, 42.68…

bayestestR::describe_posterior(results1, ci = 0.95)

## # Description of Posterior Distributions
## 
## Parameter     | Median |           95% CI |      pd |        89% ROPE | % in ROPE
## ---------------------------------------------------------------------------------
## placebo_rate  |  0.002 | [ 0.002,  0.003] | 100.00% | [-0.100, 0.100] |       100
## vaccine_rate  |  0.001 | [ 0.001,  0.002] | 100.00% | [-0.100, 0.100] |       100
## placebo_cases | 34.000 | [21.000, 53.000] | 100.00% | [-0.100, 0.100] |         0
## vaccine_cases | 19.000 | [10.000, 34.000] | 100.00% | [-0.100, 0.100] |         0
## diff_rate     | 43.205 | [ 8.409, 71.530] |  98.02% | [-0.100, 0.100] |         0

Given our data and 40,000 samples and assuming we had zero prior knowledge or estimation of effectiveness, then we have a median estimate of the % difference in infection rates = 43.205. That’s about what we would expect given our earlier investigation. The columns we really want to use are the “95% CI” and “pd” columns for diff_rate. CI in a bayesian framework is credible interval not confidence interval. Since 95% of our chains wind up in that interval we can say given our data there’s a 95% probability that diff_rate lies in its range. No, they are not the same thing as a confidence interval. The Probability of Direction (pd) is an index of effect existence, ranging from 50% to 100%, representing the certainty with which an effect goes in a particular direction (i.e., is positive or negative). We can be very confident that the vaccine does have a positive effect.

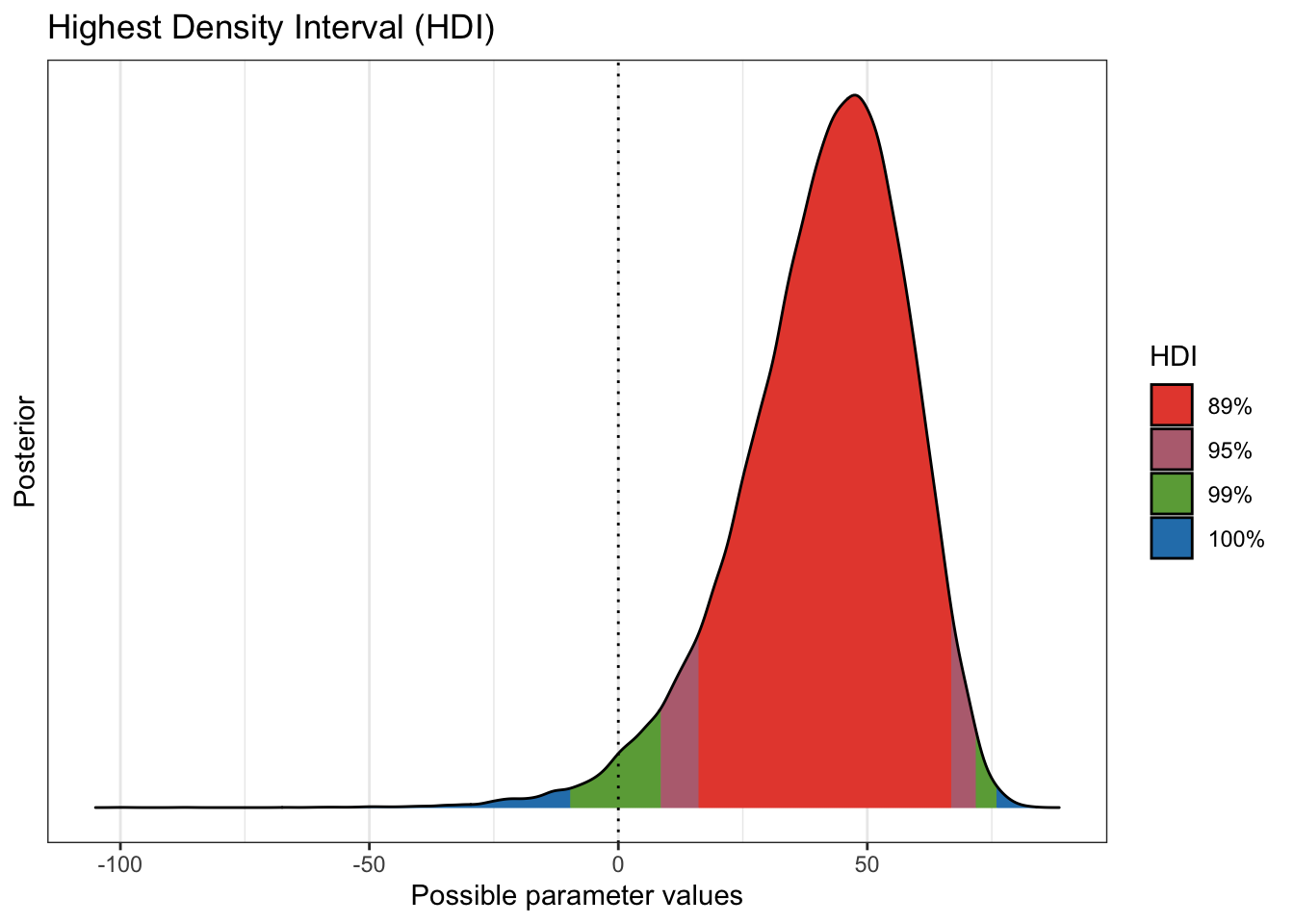
Plotting the distribution or range of diff_rate may also help the reader “see” the results. With the data we have (and remember I have been using a 19/34 split) you can see that while there’s a chance that the vaccine has no effect the evidence (the data) supports the notion that it does.

plot(bayestestR::hdi(results1$diff_rate, 
                     ci = c(.89, .95, .99)
                     )
     )