More Bayes and multiple comparisons
In my last post I had a little fun comparing perspectives among Bayesian, frequentist and programmer methodologies. I took a nice post from Anindya Mozumdar from the R Bloggers feed and investigated the world’s fastest man. I’ve found that in writing these posts two things always happen. I learn a lot, and I have follow-on questions or thoughts. This time is no exception, the last post made me want to investigate further the notion of hypothesis testing and multiple comparisons, especially in a Bayesian framework. So here we go again.
This post assumes that you’ve read the earlier posts.
Let’s quickly create our dataset following the same methodology as the last two
times, with the important exception that we’re going to focus on only the 3
fastest runners. Everything I’m going to do is extensible beyond that, but for
simplicity sake we’ll limit ourselves to just three runners. We’ll load the
required packages (suppressing the chatty load process) and create our dataset,
this time named best3 to reflect the fact we’ve reduced ourselves down to the
3 runners with the fastest mean time, Usain Bolt, Asafa Powell, and Yohan
Blake. So we have a tibble with 273 rows with the runner’s name and how fast
they ran.
library(rvest)
library(readr)
library(tidyverse)
library(ggstatsplot)
library(jmv)
library(BayesFactor)
library(gtools)
library(kableExtra)
male_100_html <- read_html("http://www.alltime-athletics.com/m_100ok.htm")
male_100_pres <- male_100_html %>%
html_nodes(xpath = "//pre")
male_100_htext <- male_100_pres %>%
html_text()
male_100_htext <- male_100_htext[[1]]
male_100 <- read_fwf(male_100_htext, skip = 1, n_max = 3178,
col_types = cols(.default = col_character()),
col_positions = fwf_positions(
c(1, 16, 27, 35, 66, 74, 86, 93, 123),
c(15, 26, 34, 65, 73, 85, 92, 122, 132)
))
best3 <- male_100 %>%
select(X2, X4) %>%
transmute(timing = X2, runner = X4) %>%
mutate(timing = gsub("A", "", timing),
timing = as.numeric(timing)) %>%
filter(runner %in% c("Usain Bolt", "Asafa Powell", "Yohan Blake")) %>%
mutate_if(is.character, as.factor) %>%
droplevels
best3$runner <- fct_reorder(best3$runner, best3$timing)
best3## # A tibble: 282 x 2
## timing runner
## <dbl> <fct>
## 1 9.58 Usain Bolt
## 2 9.63 Usain Bolt
## 3 9.69 Usain Bolt
## 4 9.69 Yohan Blake
## 5 9.72 Usain Bolt
## 6 9.72 Asafa Powell
## 7 9.74 Asafa Powell
## 8 9.75 Yohan Blake
## 9 9.75 Yohan Blake
## 10 9.76 Usain Bolt
## # … with 272 more rowsThe frequentist and multiple comparisons
Last time I chose to look at both parametric and non parametric versions of the
oneway analysis of variance. For brevity’s sake this time I am only going to run
the parametric version so I can focus on Bayesian methods in a later section.
Once again I’m going to use ggstatsplot::ggbetweenstats to combine a whole
bunch of processes that you could also do in base R. The difference is
ggbetweenstats will quickly and efficiently give us not only the tests we need
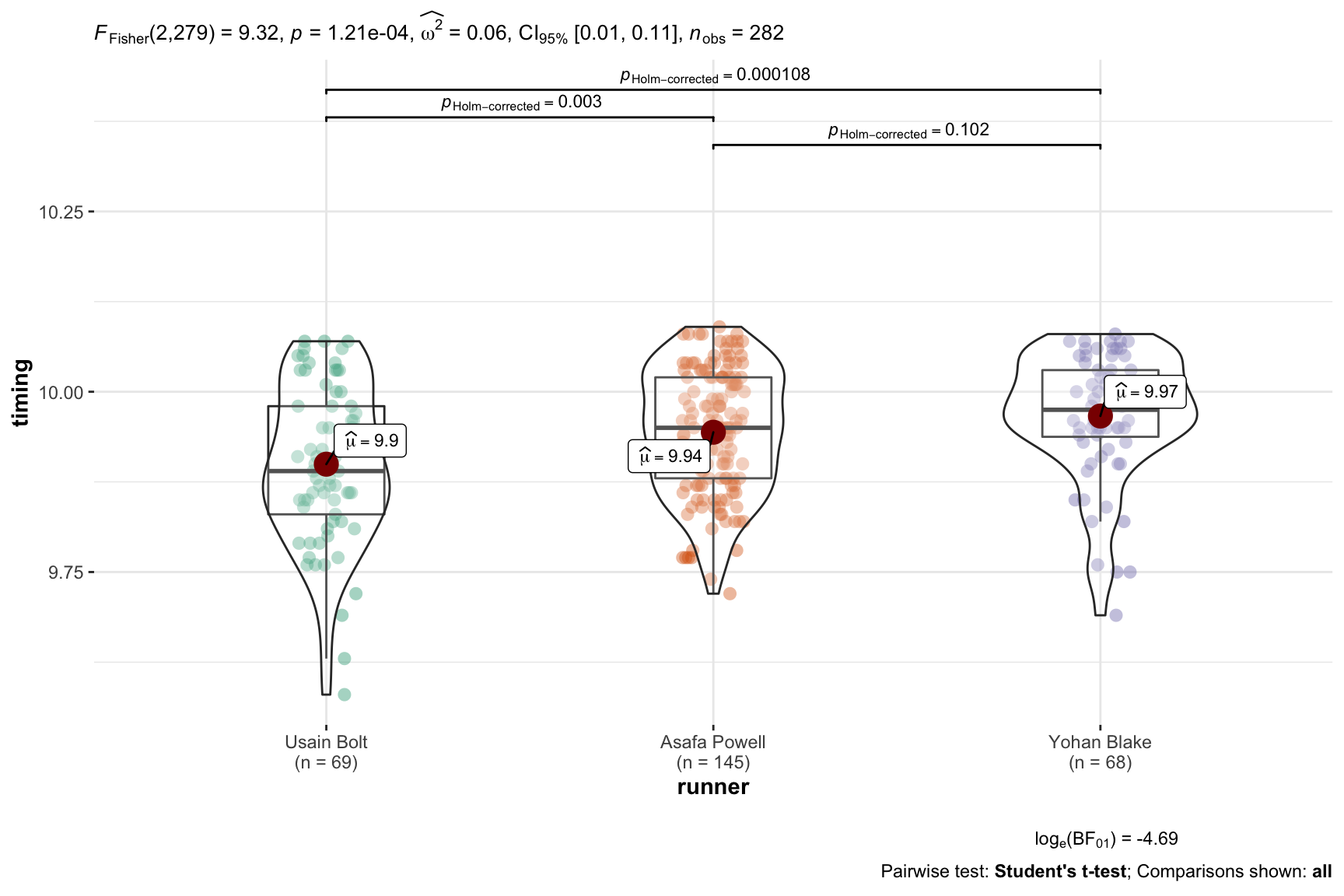
but let us visualize the data at the same time. We’ll run the required omnibuds F
test to determine whether we can reject the null h0 that all the runners
have the same mean time. Which is the required first step in nhst when you
have more than two factor levels in your dependent variable. At the same time
we’ll use the parameters pairwise.comparisons = TRUE and pairwise.display = "all" to display graphically our ability to reject the h0 that all of the
three possible pairings are different. This is in fact actually what we are most
likely interested in for our research. Just for completeness we’ll follow-up
with the base command pairwise.t.test to show the pairwise comparisons.
ggbetweenstats(data = best3,
x = runner,
y = timing,
type = "p",
var.equal = TRUE,
pairwise.comparisons = TRUE,
pairwise.display = "all",
partial = FALSE,
effsize.type = "unbiased",
point.jitter.height = 0,
messages = FALSE
)
pairwise.t.test( x = best3$timing, # outcome variable
g = best3$runner, # grouping variable
p.adjust.method = "holm" # which correction to use?
)##
## Pairwise comparisons using t tests with pooled SD
##
## data: best3$timing and best3$runner
##
## Usain Bolt Asafa Powell
## Asafa Powell 0.00255 -
## Yohan Blake 0.00011 0.10163
##
## P value adjustment method: holmYou’ve no doubt noticed that holm appears in both versions of the output. And that’s where we want to focus for now. The Holm method or correction is one of many (and by many I do mean many) ways of correcting for the fact that as we make more and more comparisons we increase the chances that we’ll reject the null when we shouldn’t.
Key take-aways
Whole books can and have been written just on the issue of multiple comparisons or simultaneous inference so I’m not going to try and summarize it all in one little blog post. I will however, for the impatient reader, summarize a few key things:
Planned versus unplanned comparisons matter in principle. In the literature you’ll see a clear distinction between making comparisons based upon clear hypothesis you’ve specified
a priorversus things donepost hoc. You are traditionally granted far more leeway if you’ve specified a small number of contrasts of interest in advance versus entered into a fishing expedition after the data are collected. Note that the math doesn’t change.The quantity of comparisons matters a great deal. Every additional pairwise comparison increases your risk of making a Type I error (rejecting h0 when you shouldn’t). From a frequentist perspective this is very bad since the entire methodology is based upon statements about controlling for type I errors.
Being more conservative about controlling against Type I error comes at the cost of risking more type II errors, failing to reject h0 when you should.
In principle there are now two distinct approaches to multiple comparisons, the traditional Family Wise Error Rate approach which you’ll see in base R with names like
"holm", "hochberg", "hommel", "bonferroni". Then there are relatively newer methods such as “BH” (Benjamini & Hochberg (1995)), and “BY” (Benjamini & Yekutieli (2001)) which control for False Discovery Rate.
Okay enough theory, let’s use our current data about the best 3 runners and see what happens across a selection of these methods.
What does that look like with our data
First off, we need to get the paired comparisons in some useful format like a
data frame that we can work with. Enter the jmv package. It has an ANOVA
(note the capitalization) function that we can make use of:
jmv::ANOVA(formula = timing ~ runner,
data=best3,
postHoc = ~runner,
postHocCorr = "none")##
## ANOVA
##
## ANOVA - timing
## ──────────────────────────────────────────────────────────────────────────────
## Sum of Squares df Mean Square F p
## ──────────────────────────────────────────────────────────────────────────────
## runner 0.1614084 2 0.080704197 9.321641 0.0001206
## Residuals 2.4155051 279 0.008657724
## ──────────────────────────────────────────────────────────────────────────────
##
##
## POST HOC TESTS
##
## Post Hoc Comparisons - runner
## ────────────────────────────────────────────────────────────────────────────────────────────────────────────
## runner runner Mean Difference SE df t p
## ────────────────────────────────────────────────────────────────────────────────────────────────────────────
## Usain Bolt - Asafa Powell -0.04429685 0.01360819 279.0000 -3.255162 0.0012730
## - Yohan Blake -0.06675831 0.01589949 279.0000 -4.198771 0.0000361
## Asafa Powell - Yohan Blake -0.02246146 0.01367582 279.0000 -1.642422 0.1016291
## ────────────────────────────────────────────────────────────────────────────────────────────────────────────Very nice looking, but all I really want is the post hoc section and I want it
as a dataframe not in pretty printed format. Turns out
anovaresults$postHoc[[1]]$asDF will give me that.
anovaresults <- ANOVA(formula = timing ~ runner,
data=best3,
postHoc = ~runner,
postHocCorr = "none")
paired_results <- anovaresults$postHoc[[1]]$asDF
paired_results## runner1 sep runner2 md se df t
## 1 Usain Bolt - Asafa Powell -0.04429685 0.01360819 279 -3.255162
## 2 Usain Bolt - Yohan Blake -0.06675831 0.01589949 279 -4.198771
## 3 Asafa Powell - Yohan Blake -0.02246146 0.01367582 279 -1.642422
## pnone
## 1 1.273009e-03
## 2 3.612892e-05
## 3 1.016291e-01Armed with that I can proceed to clean it up a bit and do some relabeling…
paired_results <- paired_results %>%
select(-df) %>%
mutate(Pair = str_c(runner1,sep,runner2)) %>%
rename(meandif = md, stderr = se, tvalue = t) %>%
mutate_at(vars(meandif, stderr, tvalue), round, 3) %>%
select(Pair, meandif, stderr, tvalue, pnone)
paired_results## Pair meandif stderr tvalue pnone
## 1 Usain Bolt-Asafa Powell -0.044 0.014 -3.255 1.273009e-03
## 2 Usain Bolt-Yohan Blake -0.067 0.016 -4.199 3.612892e-05
## 3 Asafa Powell-Yohan Blake -0.022 0.014 -1.642 1.016291e-01Pair is self-explanatory and pnone contains the unadjusted probability of
the t-test for that pairing. What we want to do next is to append the
results for the various adjustment methods onto paired_results.
p.adjust.methods contains a vector with the names we have to choose from.
Since we already have the value for none let’s leave that out, and since
fdr and BH are identical let’s remove fdr. Armed with our list of
methods we’d like to try we can use sapply to iterate through our uncorrected
p values and produce a nice matrix with rounded values and store them in
p.adj.
p.adjust.methods## [1] "holm" "hochberg" "hommel" "bonferroni" "BH"
## [6] "BY" "fdr" "none"p.adjust.M <- p.adjust.methods[p.adjust.methods %in% c("bonferroni",
"holm",
"hochberg",
"hommel",
"BH",
"BY")]
p.adj <- sapply(p.adjust.M,
function(meth) round(p.adjust(paired_results$pnone, meth), 3))
p.adj## holm hochberg hommel bonferroni BH BY
## [1,] 0.003 0.003 0.003 0.004 0.002 0.004
## [2,] 0.000 0.000 0.000 0.000 0.000 0.000
## [3,] 0.102 0.102 0.102 0.305 0.102 0.186Then we can graft those values onto the paired_results we have, do a little
more cleanup and voila we have a nice table that allows us to look at all the
data. I’ve taken the liberty of adding a header row to distinguish between FWER
and FDR methods.
pairs_compare <- cbind(paired_results, as.data.frame(p.adj))
pairs_compare <- pairs_compare %>%
mutate(p.unadj = round(pnone,3)) %>%
select(-pnone)
# pairs_compare # skip ordinary output in favor of nicer kable table
kable(pairs_compare, "html") %>%
kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive")) %>%
add_header_above(c(" " = 4, "FWER" = 4, "FDR" = 2, "None" = 1), bold = TRUE, italic = TRUE)| Pair | meandif | stderr | tvalue | holm | hochberg | hommel | bonferroni | BH | BY | p.unadj |
|---|---|---|---|---|---|---|---|---|---|---|
| Usain Bolt-Asafa Powell | -0.044 | 0.014 | -3.255 | 0.003 | 0.003 | 0.003 | 0.004 | 0.002 | 0.004 | 0.001 |
| Usain Bolt-Yohan Blake | -0.067 | 0.016 | -4.199 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Asafa Powell-Yohan Blake | -0.022 | 0.014 | -1.642 | 0.102 | 0.102 | 0.102 | 0.305 | 0.102 | 0.186 | 0.102 |
Notice that for our data, the choice of method doesn’t lead to any different conclusion. We can always reject the null that Bolt vs Blake or Bolt vs Powell is equal. And no method leads us to be able to reject the possibility that Powell vs Blake is equal.
More importantly though, we’re probably not really answering the most important question(s).
Asking different questions, differently
As I mentioned last post I’m becoming both more comfortable with using Bayesian methods and more convinced they do a better job of answering the research questions we’re really interested in. Instead of rejecting the null as a yes/no decision at some level of \(\alpha\) = .05, .01 or .001 the Bayesian wants to know what are the odds, given our data, that my research question h1 is supported. So we can ask the same question of the oneway anova with…
bf1 <- anovaBF(timing ~ runner, data = best3)
bf1## Bayes factor analysis
## --------------
## [1] runner : 144.1756 ±0.03%
##
## Against denominator:
## Intercept only
## ---
## Bayes factor type: BFlinearModel, JZSWhich allows us to say the evidence provided by the data corresponds to odds of 7:1 that the runners are not equally fast. As I mentioned last post that is actually a marked improvement in and of itself. But wait there’s more. Obviously we’re not really interested in a blanket statement about at least one being faster than the others we want to know how they compare at the paired level, analogous to paired comparisons for a frequentist.
One of the other nice features about a Bayesian approach is that we don’t have
to worry nearly as much about the multiple comparisons issue Gelman, Hill,
Yajima
(2012).
So let’s use the ttestBF function to calculate the BF for each of our 3
pairings in question and append them to our existing dataframe pairs_compare.
N.B. Before anyone comments yes the code below absolutely screams out asking
to be turned into one of more functions. And I will, one of these days, but for
now please permit me some laziness. Or if it truly offends you feel free to
write the code yourself and send it to me.
We’ll create an empty vector to hold our 3 Bayes Factors we’re going to
calculate. We’ll take best3 and filter out for just the pair we want. Run
ttestBF. Extract just the Bayes Factor using extractBF %>% .$bf and put it
in the vector. Add a column to the dataframe rounding as we go
pairs_compare$BFfactor <- round(bfpaired,1). Display the results in a pretty
table.
# create an empty vector with length of three
bfpaired <- numeric(3)
# calculate the bfs one by one enter them in vector
bfpaired[1] <- best3 %>% filter(runner %in% c("Usain Bolt", "Asafa Powell")) %>%
droplevels %>%
as.data.frame %>%
ttestBF(formula = timing ~ runner, data = .) %>%
extractBF %>%
.$bf
bfpaired[2] <- best3 %>% filter(runner %in% c("Usain Bolt", "Yohan Blake")) %>%
droplevels %>%
as.data.frame %>%
ttestBF(formula = timing ~ runner, data = .) %>%
extractBF %>%
.$bf
bfpaired[3] <- best3 %>% filter(runner %in% c("Asafa Powell", "Yohan Blake")) %>%
droplevels %>%
as.data.frame %>%
ttestBF(formula = timing ~ runner, data = .) %>%
extractBF %>%
.$bf
# round and append the values as a column named BF10
pairs_compare$BF10 <- round(bfpaired,1)
# make a pretty table
kable(pairs_compare, "html") %>%
kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive")) %>%
add_header_above(c(" " = 4, "FWER" = 4, "FDR" = 2, "None" = 1, "Bayes" = 1))| Pair | meandif | stderr | tvalue | holm | hochberg | hommel | bonferroni | BH | BY | p.unadj | BF10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Usain Bolt-Asafa Powell | -0.044 | 0.014 | -3.255 | 0.003 | 0.003 | 0.003 | 0.004 | 0.002 | 0.004 | 0.001 | 17.0 |
| Usain Bolt-Yohan Blake | -0.067 | 0.016 | -4.199 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 163.5 |
| Asafa Powell-Yohan Blake | -0.022 | 0.014 | -1.642 | 0.102 | 0.102 | 0.102 | 0.305 | 0.102 | 0.186 | 0.102 | 0.7 |
Bolt vs the other two runners yields no surprise. It quantifies the degree to which our evidence supports our hypothesized relationship but given the frequentist’s results we’re not surprised just happy to be able to make more probability based statements.
But Powell vs Blake is slightly disconcerting. The odds are 0.2924466 : 1 that Powell is faster than Blake? Now is the point at which we need to remember that one of the other benefits of a Bayesian approach is that it quantifies support for both the research hypothesis, which bayesians label BF10, as well as support for the null hypothesis called BF01! Therefore we can interpret that BF = .3 (rounded) as being the evidence provided by the data corresponds to odds of (1/0.2924466) BF01 = 3:1 that the runners ARE equally fast.
Even more nuance
But IMHO one of the most impressive things about the bayesian methodology is the ability to build complex models and to truly ask questions that are what you’re interested in and how the data support (or not) rather than simply rejecting a null hypothesis.
The next example benefited greatly from this
post by the author of
the BayesFactor package, Richard Morey. We’re not really interested in generic
hypotheses that various runners aren’t equal. Oh no, as we sit in the bar we’re
really interested in a very specific question. Our hypothesis is that if we were
to arrange the dream race of the century and get Bolt, Powell and Blake on the
100m track that the finishing order would be Bolt first, Powell second and Blake
third. The data when we view them visually seem to point us in that direction
but it would be nice to get some sense of what the odds really are. We already
have an empirical answer to one model stored in bf1 where the BF10 =
144.1756106. Let’s start constructing a model that honors our actual
question.
Our first step is to determine what we think our priors are before we have seen
our data. Let’s take the view that we know nothing about male 100m runners and
simply assume the runners have an equal chance of winning, I mean after all they
are three of the fastest, if not the fastest, men alive. Three runners, how many
different unique ways are there for them to finish (assuming ties are not
possible)? The answer is quite simple but I’m going to code it out in r just so
I have code for a future more complicated case. The gtools::permutations
function allows us to map out all the possible unique finishing orders for our 3
runners. There are 6. Of the 6 only row #3 is what we are hypothesizing, none of
the others match our research hypothesis. So our prior probabilities are 1/6 and
we’ll store that in prior_odds_h1. Yes I know the code snippet below is
overkill for the current problem and prior_odds_h1 <- 1 / 6 would have gotten
me there faster without having to resort to loading the gtools package but I
wanted to lay out a methodology for the future and possibly more complex cases.
possible_finishes <- permutations(n = 3, r = 3, v = unique(levels(best3$runner)))
possible_finishes## [,1] [,2] [,3]
## [1,] "Asafa Powell" "Usain Bolt" "Yohan Blake"
## [2,] "Asafa Powell" "Yohan Blake" "Usain Bolt"
## [3,] "Usain Bolt" "Asafa Powell" "Yohan Blake"
## [4,] "Usain Bolt" "Yohan Blake" "Asafa Powell"
## [5,] "Yohan Blake" "Asafa Powell" "Usain Bolt"
## [6,] "Yohan Blake" "Usain Bolt" "Asafa Powell"prior_odds_h1 <- 1 / nrow(possible_finishes)
prior_odds_h1## [1] 0.1666667Okay we managed to get our “prior” with some very simple knowledge and math. To
compute a posterior is a little trickier, and we’re going to need our friend the
programmer to help us simulate some to get the answer. The bf1 object we
created earlier has some useful information in it. A mathematical model formula
for our posterior distribution. But it doesn’t allow us to directly generate the
posterior probability we need to proceed. I’m not even going to try and
explain the math but this post might
help. For now in this little
post I’m simply going to be satisfied with showing you how to use the
posterior function in the BayesFactor package to come up with a reasonable
and stable estimate.
Let’s set a random seed for reproducibility (on the chance you want your answer
to match mine else you’re likely to get a slightly different answer every time
because we are sampling). Use the posterior function and take a look at what we
get. Focus on the column labeled mu (the grand mean for all 3 runners),
and the columns labelled for each runner like runner-Usain Bolt which are
how their mean time differed from the overall mean mu. A negative in this
case indicates faster than the group mean. So we have 10,000 random simulations,
and for each one we have a simulated draw from our data.
set.seed(1234)
samples <- posterior(bf1, iterations = 10000)
head(samples)## Markov Chain Monte Carlo (MCMC) output:
## Start = 1
## End = 7
## Thinning interval = 1
## mu runner-Usain Bolt runner-Asafa Powell runner-Yohan Blake
## [1,] 9.860199 0.03941820 -0.0256338656 -0.01378433
## [2,] 9.937739 -0.02548752 -0.0123985442 0.03788606
## [3,] 9.925944 -0.02800456 0.0006957551 0.02730881
## [4,] 9.941116 -0.02558670 0.0051795110 0.02040719
## [5,] 9.936720 -0.02789285 0.0041579517 0.02373490
## [6,] 9.940669 -0.05242072 0.0070606025 0.04536012
## [7,] 9.937666 -0.03155442 -0.0044185658 0.03597299
## sig2 g_runner
## [1,] 0.022299952 0.1726095
## [2,] 0.009297112 0.4232915
## [3,] 0.010127386 0.3618486
## [4,] 0.008350989 0.1429471
## [5,] 0.008973504 0.8421863
## [6,] 0.010552894 0.6322548
## [7,] 0.008594494 3.7694861To get our estimate of the posterior probability then given our data and our
model, all we have to do is count! What should we count? Well our hypothesis
H1 is that when we look at timing Bolt < Powell < Blake. So let’s write
some r code to run through the 10,000 rows label each row TRUE if it supports
our H1 and FALSE if it doesn’t. Then we can use sum to count the
“TRUES”. Once we have that count our posterior probability for our research
hypothesis becomes the number that support divided by the total number of tries
10,000.
consistent_with_h1 <- (samples[, "runner-Usain Bolt"] < samples[, "runner-Asafa Powell"]) &
(samples[, "runner-Asafa Powell"] < samples[, "runner-Yohan Blake"])
head(consistent_with_h1, 20)## [1] FALSE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE FALSE TRUE TRUE
## [13] TRUE FALSE TRUE TRUE TRUE TRUE TRUE TRUEN_consistent_with_h1 <- sum(consistent_with_h1)
N_consistent_with_h1## [1] 9332posterior_prob_h1 <- N_consistent_with_h1 / nrow(samples)
posterior_prob_h1## [1] 0.9332Now to calculate the Bayes Factor for this very specific and directional hypothesis all we need do is divide our posterior probability (our probability after seeing the data) by our prior prob which was our thing before we saw the data. The larger the BF10 the more the evidence is persuading us that our model is “correct”.
bf__h1 <- posterior_prob_h1 / prior_odds_h1
bf__h1## [1] 5.5992Using Kass and Raftery (1995) guidelines we have “Positive evidence”
| Bayes factor value | Interpretation |
|---|---|
| 1 - 3 | Negligible evidence |
| 3 - 20 | Positive evidence |
| 20 -150 | Strong evidence |
| >150 | Very strong evidence |
It’s left to you to determine just how you feel about 5:1 odds. I suppose it would depend on what the stakes were and how convinced you needed to be.
Just a little farther
Before I end this post I want to accomplish two more things that I will address next post. The first is simply a way of encouraging you to make sure you understand this methodology. When you look at the distribution of the data plotted near the beginning of the post your eyes should “tell” you that while it is pretty clear Bolt is fastest the difference between Powell and Blake is quite small. Therefore the most likely reason we “only” get a BF of approximately 5:1 is the second part of our hypothesis Powell < Blake. So my challenge to you is to take the code and change it to make your research hypothesis that Bolt < Powell and that Bolt < Blake but make no assertion about Powell and Blake. hint - pay attention to your prior too. My next post I’ll address this and an even more complicated hypothesis.
Second, sometimes you want to compare nested models. If we think of the values
stored in bf1 as our “full model” i.e., is any runner faster than any other
runner in any direction we had a BF = ~7:1. Our more specific model gave us
~5:1. Bayes Factors are transitive and we can multiply them together to give us
a sense of improvement very easily…
## extract just the BF from bf1 so that we can multiply it
bf_full_model <- as.vector(bf1)
bf_full_model## runner
## 144.1756## Use transitivity to compute a comparative Bayes factor
bf_comparing <- bf__h1 * bf_full_model
bf_comparing## runner
## 807.2681Done
I want to end here today and follow up next week in an additional post. I hope you’ve found this useful. I am always open to comments, corrections and suggestions. Feel free to leave a comment in disqus or send me an email.
Chuck
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License

