I didn't mean() to ignore the median()

library(tidyverse)
library(BayesFactor)
library(ggsignif)
library(scales)

theme_set(theme_bw()) # set theme

location <- "https://github.com/WinVector/PDSwR2/raw/master/PUMS/incomedata.rds"
incomedata <- readRDS(url(location))

incomedata$gp <- NULL

incomedata$employment <- fct_recode(incomedata$employment,
  "Self Not Inc" = "Self employed not incorporated",
  "Self Incorporated" = "Self employed incorporated",
  "Private for Profit" = "Employee of a private for profit",
  "Private Non Profit" = "Private not-for-profit employee",
  "Federal Government" = "Federal government employee",
  "State Government" = "State government employee",
  "Local Government" = "Local government employee"
)

incomedata$employment <- forcats::fct_reorder(
  .f = incomedata$employment,
  .x = incomedata$income, 
  .fun = mean
)


# In case I want to reduce down to 3 more fundamental
# categories Private, Government, or self employed
incomedata$empcategory <- fct_collapse(incomedata$employment,
  "Self" = c("Self Not Inc", "Self Incorporated"),
  "Private" = c("Private for Profit", "Private Non Profit"),
  "Government" = c("Federal Government", "State Government", "Local Government")
)

str(incomedata)

## 'data.frame':    22241 obs. of  6 variables:
##  $ income     : num  22000 21000 25800 25000 20200 36000 20000 30000 23000 5000 ...
##  $ age        : num  24 31 26 27 27 47 24 41 43 21 ...
##  $ sex        : Factor w/ 2 levels "Male","Female": 1 2 2 2 2 1 1 1 2 2 ...
##  $ employment : Factor w/ 7 levels "Self Not Inc",..: 2 4 2 2 4 2 2 2 2 2 ...
##  $ education  : Factor w/ 9 levels "no high school diploma",..: 1 4 4 6 4 2 1 1 6 2 ...
##  $ empcategory: Factor w/ 3 levels "Self","Private",..: 2 2 2 2 2 2 2 2 2 2 ...

psych::describeBy(incomedata$income, 
                  group = incomedata$employment, 
                  mat = TRUE, 
                  digits = 2) %>%
  mutate(.data = ., 
         Employment_Type = group1,
         trimmed_mean = trimmed) %>%
  select(Employment_Type, 
         mean, 
         sd,
         median, 
         skew,
         n,
         trimmed_mean)

##      Employment_Type     mean       sd median skew     n trimmed_mean
## 1       Self Not Inc 41382.50 34209.02  30000 1.73   829     35792.72
## 2 Private for Profit 51163.99 38744.57  40000 1.82 16170     44932.92
## 3   State Government 52612.39 29331.94  47150 1.64  1028     49269.63
## 4 Private Non Profit 52996.20 34389.69  45000 1.85  1573     48085.83
## 5   Local Government 53720.47 29438.20  48000 1.29  1492     50763.72
## 6 Federal Government 65311.26 34790.20  60000 0.73   580     62641.60
## 7  Self Incorporated 66906.44 51983.28  50000 1.52   569     58579.12

We’re skewed! How do we fix it?

There are any number of ways we can address the skew issue (I won’t try methods such as: hoping your reader/reviewer is inattentive or praying to your favorite deity). When I say any number I mean a lot of different ways we can address the issue. While non-exhaustive they generally lump into one of three categories. We can trim, we can transform, or we can use non-parametric methods (which is a bit disingenuous since some of the non-parametric methods themselves rely on transforming our data – we’ll get to that in a minute). Let’s briefly discuss.

1. Trim. We can “trim” the high and lows hoping this will eliminate any troubling values at both ends. You may be surprised to know that capability is built into mean() in base R, and mean(incomedata$income, , trim = .1) will work. For those of you paying attention I grabbed that info when I ran psych::describeBy. As you would expect for each of our groups it has produced a trimmed mean which is closer to the median than our original mean. My problem with it is threefold. I hate throwing away data. In this case we have plenty but still. Second, there is no one right answer as to how much we should trim? Why .1? Why not .05 or .2? It can make you suspicious that we are simply picking an amount of trimming that best serves our agenda. Finally, it implicitly makes the extreme values wrong or invalid or “not right”. In this case there is little evidence that this is true. The income values don’t look impossible or wrong, they just seem to reflect that there are people who make much more and that zero is as low as it goes. Personally I tend to only use trimming when I think the measurement is producing bad values typically on both ends of the spectrum.

2. Transform. One of the common solutions to the income data problem is to transform the variable. The transformation can take the form of a square root, a log, or a more complex method such as Box-Cox or Yeo-Johnson. The later is especially useful if your variable can validly take on negative values (negative income anyone?). All of these methods are likely to “fix” our positive skew problem since they will all serve to “pull” our data to the left in a consistent way. All of them make it more difficult to describe our results since for many readers the log of income is not a natural concept. The other limitation here is that there is no one approved transform all will serve to “improve” our skew but we’re subject to being questioned as to why we selected one unless it is a disciplinary custom or for reasons of comparison.

3. Non-parametric. For our particular case there are two non parametric methods we would select. For the overall comparison of income across the 7 levels of Employment it would be the Kruskal-Wallis. For pairwise comparisons as we did last post it would be the Mann-Whitney U (a.k.a. Wilcoxon rank sum) test. If you look back you’ll even notice that the Wilcoxon rank sum test wilcox.test() is the default for ggsignif. As I mentioned earlier these tests are actually a sort of transformation as well since they rely on the ranks of our data rather than the data itself. I admit to having a bias towards (maybe even a fondness for) non-parametric tests. While they aren’t perfect and have limitations I take a certain amount of solace in knowing that any supported findings were by using tests that at least eliminate some number of assumptions.

So after last week’s posting I went sleuthing for the Bayesian equivalent to the Mann Whitney and Kruskal-Wallis tests. Yes I recognize that with powerful software like Stan you can pretty much construct any data analysis you want but I was hoping for something more “off the shelf” something very much like BayesFactor::ttestBF. No luck, I won’t claim I searched everywhere but I did search a lot for anything already done for R. Lot’s of theoretical papers and some questions but no solutions. If I missed it, and someone knows about it, please share.

Since I have been tracking the progress of JASP (unsolicited praise – it looks like a great piece of software especially if you come from the world of SPSS which I do). A lot of the calculation that is done under the very nice GUI is powered by R code and libraries. I noticed that they had recently implemented a Bayesian version of the Mann Whitney so I decided to give it a try. No joy! Using the very same data I have been using for these blog posts it ran for well over an hour and hadn’t completed. When I came back the next day it had completed and produced what appeared to be reasonable results on the surface but I had to do some sleuthing because the very long run time had me confused.

The underlying code is open source and you can see it here. After a little bit of fiddling I was able to separate the JASP interface pieces from the R code that produces the results. I was thwarted again. Even on a much smaller dataset like ggplot2::mpg the results are slow and unstable. That’s not meant as a complaint I know they are working on it and I know working through the ties is challenging.

A Eureka and a “YouRankA”

Temporarily thwarted – something in the back of my mind made me remember dimly from the past considering the case of t tests on rankings. It had been a long time (nowadays it so trivial to run for example wilcox.test) and I wasn’t quite sure how comparable the results would be so I went looking. Found research on the frequentist side at least that the methodologies produce consistent results (Zimmerman, 2012).

So if I can’t have a mannwhitneyBF maybe I can ttestBF(rank(income))? Seemed promising and the initial results seemed to be reasonable as well. The only challenge seemed to be that the distribution of rank(anything) tends to be anything but normal. The result tends to be very very flat with almost no tails at all. Almost a uniform distribution. Hmmmmm, which is a worse violation of t-test assumptions, skewed or flat?

As I was puzzling on that I stumbled upon another avenue of exploration from a blog post by Andrew Gelman at Columbia here and here. Quoting…

“Take-home message: I am not saying that the rank-then-inverse-normal-transform strategy is always or even often a good idea. What I’m saying is that, if you were planning to do a rank transformation before analyzing your data, I recommend this z-score approach rather than the classical Wilcoxon method.” Gelman (July 2015)

That sounded promising. Was there an easy way for someone like me to implement his better than Wilcoxon suggestion (point taken that he repeatedly says “I’m not saying you should transform the data. I’m saying that if you were going to do Wilcoxon, then you’re already doing a rank transformation, in which case I think it makes sense to do it in an expandable way, rather than getting hung up on some pre-tabulated test statistics.”)?

Turns out there is. And it’s easy. And it’s already written and packaged in the RNOmni package on CRAN. The function is RankNorm and straight from the description what it does is: “Applies the rank based inverse normal transform (INT) to a numeric vector. The INT can be broken down into a two-step procedure. In the first, the observations are transformed onto the probability scale using the empirical cumulative distribution function (ECDF). In the second, the observations are transformed onto the real line, as Z-scores, using the probit function.”. The key component of the function is qnorm((r - k)/(n - 2 * k + 1)) where r is the rank, n the number of observations, and k = 3/8 = the Blom transform.

I just realized I’ve been rambling for quite some time without a single graphic or plot. Perhaps this is a good time to just display the original income data and what the various transformations would do to them. I’ll plot them as density plots and superimpose the theoretical normal curve in a different color.

Let’s use cowplot and make 7 plots in order:

1. The original income data
2. Transform income to a z score (mean = 0, sd = 1) scale(income)
3. Transform sqrt(income)
4. Transform log(income)
5. Transform VGAM::yeo.johnson(income, lambda = .1)
6. Transform rank(income)
7. Transform RNOmni::RankNorm(income)

So as a first step we’ll use the mutate function to create these new variables. We’ll deliberately name them all so they end with "_income". In a minute we’ll use that little bit of consistency to make our lives easier.

incomedata <- 
  incomedata %>%
  mutate(z_income = as.numeric(scale(income)),
         sqrt_income = sqrt(income),
         log_income = log(income),
         yj_income = VGAM::yeo.johnson(income, lambda = .1),
         rank_income = rank(income),
         rint_income = RNOmni::RankNorm(income)
         )

glimpse(incomedata)

## Rows: 22,241
## Columns: 12
## $ income      <dbl> 22000, 21000, 25800, 25000, 20200, 36000, 20000, 30000, 2…
## $ age         <dbl> 24, 31, 26, 27, 27, 47, 24, 41, 43, 21, 29, 30, 28, 43, 3…
## $ sex         <fct> Male, Female, Female, Female, Female, Male, Male, Male, F…
## $ employment  <fct> Private for Profit, Private Non Profit, Private for Profi…
## $ education   <fct> "no high school diploma", "some college credit, no degree…
## $ empcategory <fct> Private, Private, Private, Private, Private, Private, Pri…
## $ z_income    <dbl> -0.791115497, -0.817539654, -0.690703699, -0.711843025, -…
## $ sqrt_income <dbl> 148.32397, 144.91377, 160.62378, 158.11388, 142.12670, 18…
## $ log_income  <dbl> 9.998798, 9.952278, 10.158130, 10.126631, 9.913438, 10.49…
## $ yj_income   <dbl> 17.17967, 17.05353, 17.61618, 17.52934, 16.94867, 18.5516…
## $ rank_income <dbl> 3941.5, 3694.5, 5444.5, 5082.0, 3531.0, 9310.0, 3191.0, 6…
## $ rint_income <dbl> -0.9260927, -0.9697185, -0.6910214, -0.7438702, -0.999640…

A quick glimpse indicates we have what we need. So we have seven variables and we’re going to create 7 identical plots using ggplot. For each plot we’ll plot the density function for our observations (a more granular histogram so to speak). We’ll also plot the theoretical normal curve for that variable using dnorm() with the mean and standard deviation for the variable.

We could just write (mainly cut and paste) the call to ggplot 7 times. But that seems wasteful. Instead we’ll use purrr:pmap to do what we want with a lot less code. pmap wants a list that has as it’s components the 3 things that are going to vary for each of the seven iterations. The 3 things are the name of the variable, the mean, and the sd for the variable. Since ggplot can be fickle about passing it bare variable names we’ll pass it character strings for the name. The mean and the sd of course are numeric types. Again we could manually build those vectors but that would be tedious so let’s use some dplyr::select_at and summarise_at statements to get what we need. Since we were careful to name our variables so that they all end with “income” we can use vars(ends_with("income")) to grab just what we need and not all the variables in incomedata.

a <- incomedata %>% 
  select_at(vars(ends_with("income"))) %>% names 

b <- incomedata %>% 
  summarise_at(vars(ends_with("income")), mean, na.rm = TRUE) 

c <- incomedata %>% 
  summarise_at(vars(ends_with("income")), sd, na.rm = TRUE) 

plot_list <- list(
  which = a,
  means = b,
  stddevs = c
)

plot_list

## $which
## [1] "income"      "z_income"    "sqrt_income" "log_income"  "yj_income"  
## [6] "rank_income" "rint_income"
## 
## $means
##    income     z_income sqrt_income log_income yj_income rank_income
## 1 51939.1 2.884567e-17    214.8975   10.61248  18.97702       11121
##     rint_income
## 1 -4.205901e-05
## 
## $stddevs
##     income z_income sqrt_income log_income yj_income rank_income rint_income
## 1 37844.16        1    75.88434  0.7348988   2.09446    6419.503   0.9991945

That took more text to describe than it took code to enact!

Now we invoke ggplot as a function .f. Inside the function call you’ll see ..1, ..2 & ..3 those mark the places where pmap will substitute in the appropriate value of plot_list. The output of pmap is itself a list. A list of ggplot objects. We’ll take that list and give it to cowplot::plot_grid along with some labeling and formatting and voila!

list_of_plots <- pmap(.l = plot_list,
                      .f = ~ ggplot(data = incomedata,
                                    aes_string(x = ..1)
                                    ) +
                                    geom_density(alpha = .2) +
                                    stat_function(fun = dnorm, 
                                                  color = "red", 
                                                  args = list(mean = ..2, 
                                                              sd = ..3)
                                    )
                      )

cowplot::plot_grid(plotlist = list_of_plots,
                   labels = c("Income (Original)", 
                              "Z score Income",
                              "SQRT Income", 
                              "Log Income",
                              "Yeo Johnson Income",
                              "Ranked Income",
                              "Rank Inv Norm Income"), 
                   label_size = 12,
                   vjust = 1,
                   hjust = 0,
                   scale = .9)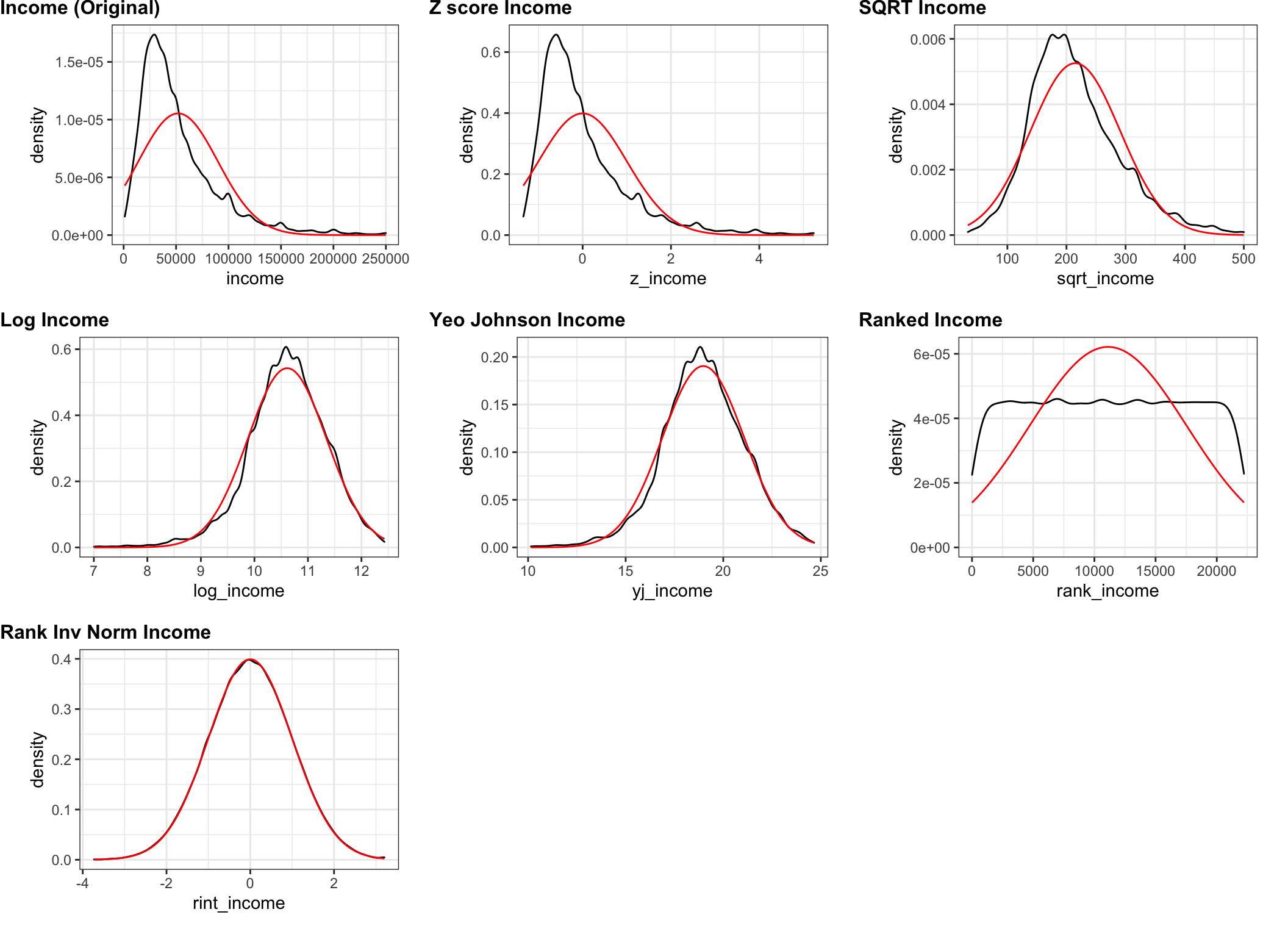

Not surprisingly the rank inverse normal transform works as advertised. We have succeeded in taking the ranks and backing them into a near perfect normal curve. That’s good but we did that work to prepare for comparing across employment groups so we would be wise to take a look at our transformed income variable rint_income by group. Once again we’ll make use of psych::describeBy. This time we’ll also include the standard deviation since we’d like to have some sense of whether the variances are at least roughly equal among the groups. While we’re at it we’ll plot the density curves on a by group basis.

psych::describeBy(incomedata$rint_income, 
                  group = incomedata$employment, 
                  mat = TRUE, 
                  digits = 2) %>%
  mutate(.data = ., 
         Employment_Type = group1,
         trimmed_mean = trimmed) %>%
  select(Employment_Type, 
         mean, 
         sd,
         median, 
         skew,
         n,
         trimmed_mean)

##      Employment_Type  mean   sd median  skew     n trimmed_mean
## 1       Self Not Inc -0.40 1.10  -0.49  0.04   829        -0.41
## 2 Private for Profit -0.04 1.02  -0.05  0.09 16170        -0.05
## 3   State Government  0.14 0.80   0.18 -0.29  1028         0.17
## 4 Private Non Profit  0.10 0.89   0.12 -0.06  1573         0.10
## 5   Local Government  0.16 0.83   0.20 -0.51  1492         0.20
## 6 Federal Government  0.43 0.88   0.54 -0.71   580         0.49
## 7  Self Incorporated  0.31 1.13   0.27  0.02   569         0.31

incomedata %>%
  ggplot(aes(x = rint_income, 
             fill = employment,
             color = employment)
         ) +
  geom_density(alpha = .2)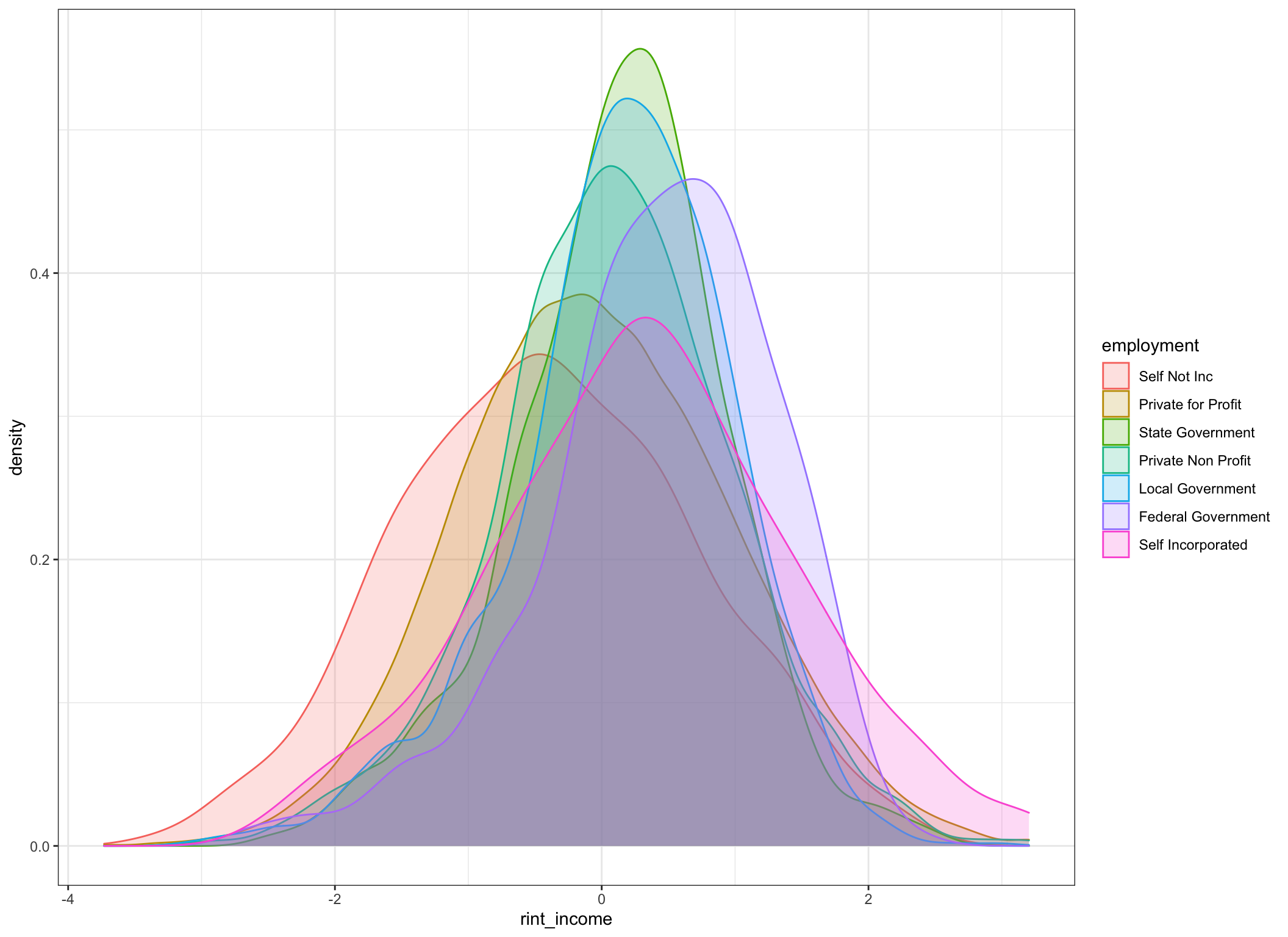

Well, we certainly seem to have improved the distributions and made them more suitable for parametric manipulation. Certainly looks like there are shifts in central tendency by group. For the astute observer yes I’ll acknowledge that the variances among groups aren’t “equal”. But an F_max ratio of 2 isn’t that awful.

From last post let’s bring back our comparisons_list function which will create a list of all the possible paired comparisons for us. We’ll store them in a list called comp.list.

comparisons_list <- function(data,
                             x) {

  data <-
    dplyr::select(
      .data = data,
      x = !!rlang::enquo(x)
      ) %>%
    dplyr::mutate(.data = ., 
                  x = droplevels(as.factor(x)))
  
  grouplevels <- levels(data$x)
  g1_list <- combn(grouplevels, 2)[1, ]
  g2_list <- combn(grouplevels, 2)[2, ]
  
  comparisons_list <- lapply(
    1:length(g1_list),
    function(i) c(
      combn(grouplevels, 2)[2, i],
      combn(grouplevels, 2)[1, i]
    )
  )
  
  return(comparisons_list)
}

comp.list <- comparisons_list(incomedata, employment)

Welcome back my friends to the show that never ends (ELP)

Last week we produced this plot using the original income data and using ggsignif. We ran the wilcox.test against all the pairings to produce p values on the plot. Here it is unretouched to refresh your memory.

If Gelman and Zimmerman have steered me correctly (or lol if I paid enough attention) we should be able to substitute in rint_income our ranked inverse normalized transformed version of income and get very similar results using the very same code and wilcox.test.

ggplot(data = incomedata, 
       aes(
         x = employment,
         y = rint_income,
         fill = employment,
         group = employment
       )) +
  geom_boxplot(show.legend = FALSE) +
  geom_signif(
    comparisons = comp.list,
    step_increase = .1
  ) +
  scale_y_continuous(breaks = seq(from = -4,
                                  to = 4, 
                                  by = 1)
                     ) +  
  ggtitle(label = "ACS 2016 Rank Inverse Transformed Income by Employer Type", 
          subtitle = "Mann Whitney multiple comparisons non directional hypothesis using wilcox.test")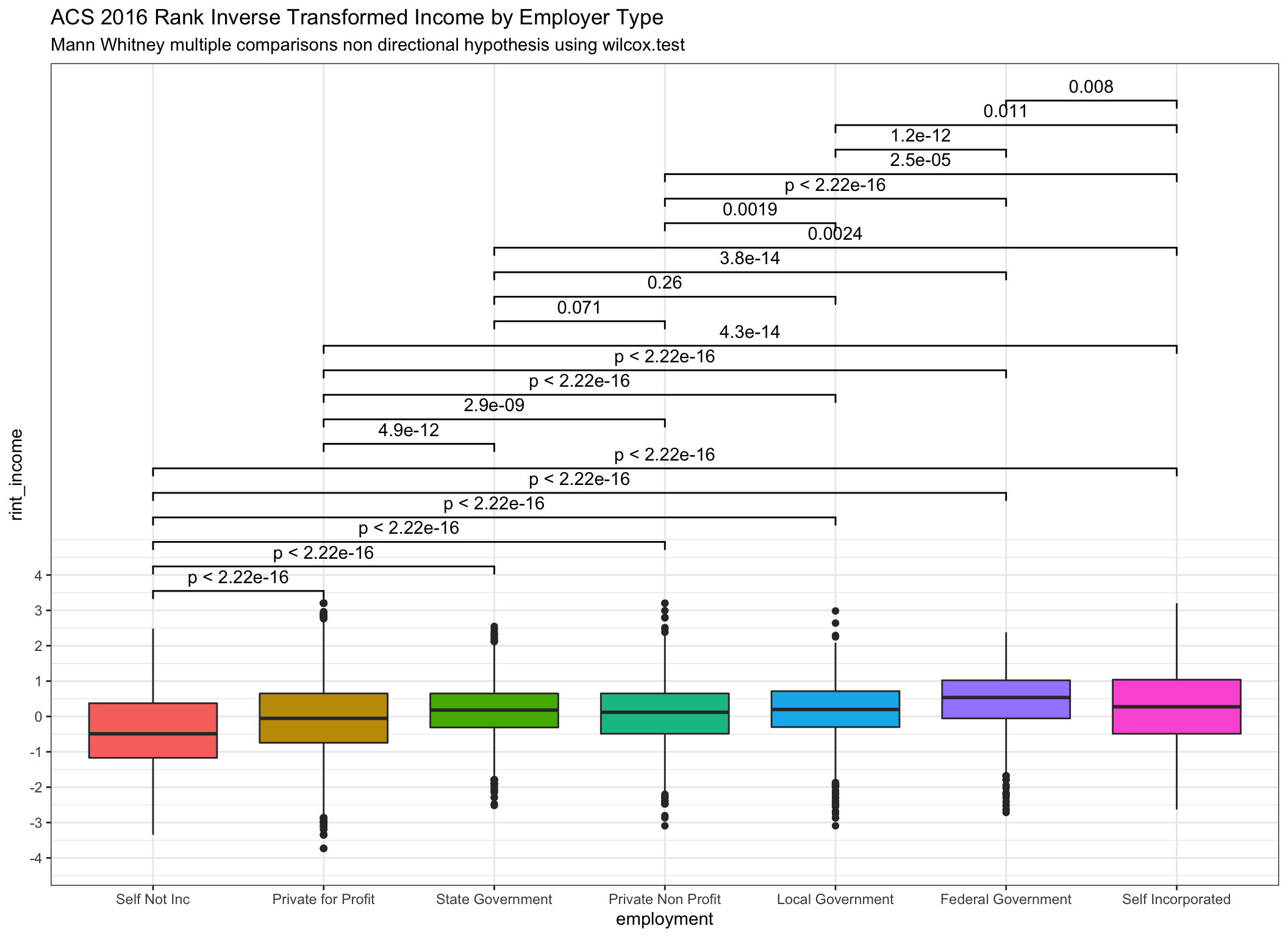 

ggplot(data = incomedata, 
       aes(
         x = employment,
         y = rank_income,
         fill = employment,
         group = employment
       )) +
  geom_boxplot(show.legend = FALSE) +
  geom_signif(
    comparisons = comp.list,
    step_increase = .1
  ) +
  scale_y_continuous(breaks = seq(from = 0,
                                  to = 25000, 
                                  by = 5000)
                     ) +  
  ggtitle(label = "ACS 2016 Ranked Income by Employer Type", 
          subtitle = "Mann Whitney multiple comparisons non directional hypothesis using wilcox.test")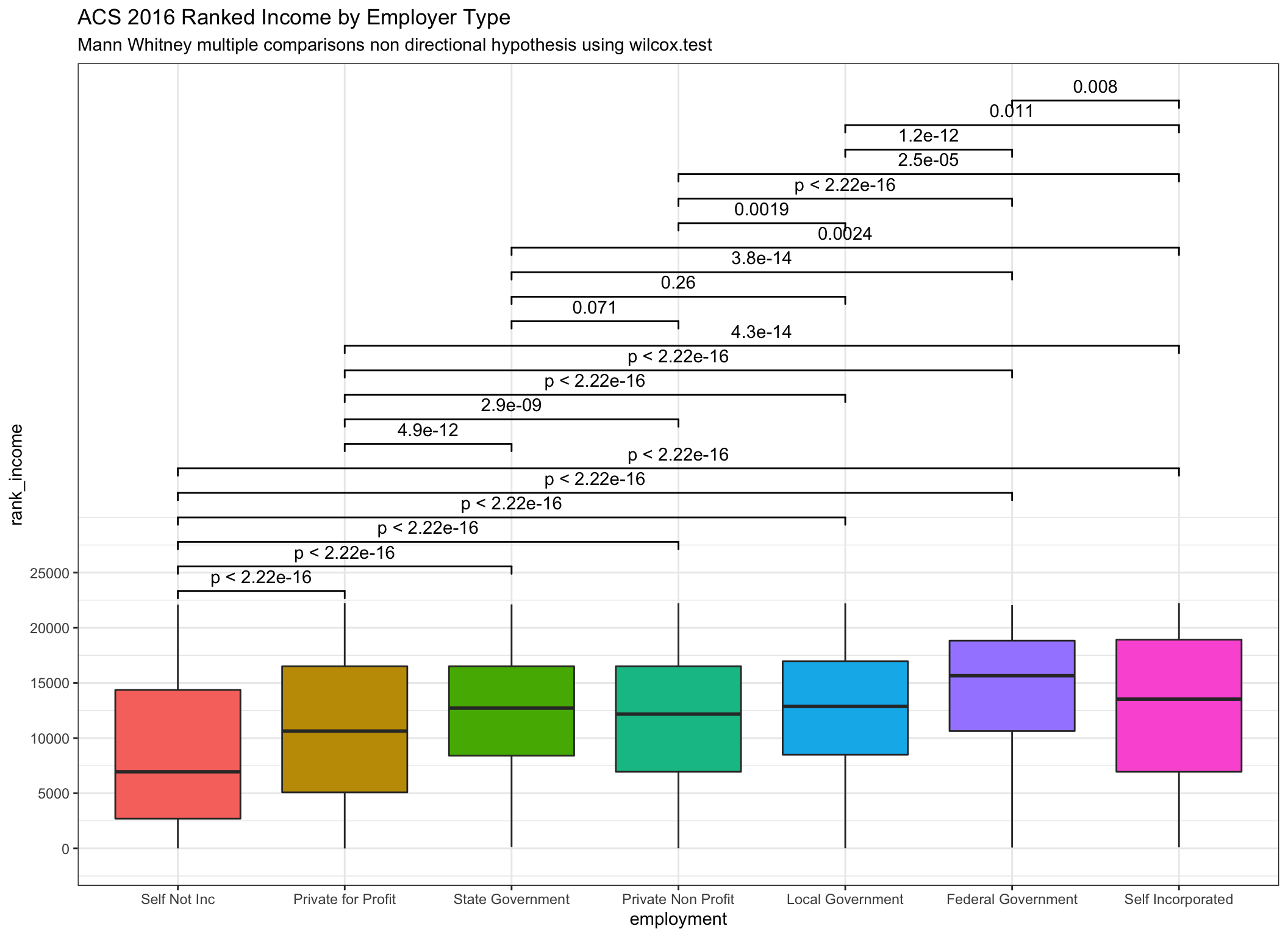 

Reminder - Note that in the two-sample case the estimator for the difference in location parameters does not estimate the difference in medians (a common misconception) but rather the median of the difference between a sample from x and a sample from y.

Very similar indeed! Notice that the reported p values are essentially identical even as we can see from the box plots that the transformations are having an effect.

But of course this has all been prep work to this point. What I’m really after is to shift over to a bayesian framework and generate bayes factors that are the equivalent of the frequentist’s Mann Whitney. So let’s get on with that!

Not having been able to find the R code to do the work directly I’ve transformed the income variable and will now apply the ttestBF function. Last post I wrote a little function called pairwise_bf that generates the bayes factors and manipulates them in a way that makes them suitable for plotting with ggplot and ggsignif. Here it is again.

pairwise_bf <- function(x = NULL,
                        y = NULL,
                        display_type = "bf",
                        k = 2) {
  results <- ttestBF(x = x, y = y) %>%
    extractBF() %>%
    mutate(support = case_when(
      bf < .01 ~ "extreme BF01",
      bf < .03 & bf >= .01 ~ "very strong BF01",
      bf < .1 & bf >= .03 ~ "strong BF01",
      bf < 1 / 3 & bf >= .1 ~ "moderate BF01",
      bf < 1 & bf >= 1 / 3 ~ "anecdotal BF01",
      bf >= 1 & bf < 3 ~ "anecdotal BF10",
      bf >= 3 & bf < 10 ~ "moderate BF10",
      bf >= 10 & bf < 30 ~ "strong BF10",
      bf >= 30 & bf < 100 ~ "very strong BF10",
      bf >= 100 ~ "extreme BF10"
    )) %>%
    mutate(logged = case_when(
      bf < 1 ~ paste("log(BF01) = ", round(log(1 / bf), k)),
      bf >= 1 ~ paste("log(BF10) = ", round(log(bf), k))
    )) %>%
    mutate(human = case_when(
      bf < .000001 ~ "BF01 >= 1,000,000 : 1",
      bf < .001 & bf >= .000001 ~ "BF01 >= 1,000 : 1",
      bf < .01 & bf >= .001 ~ "BF01 >= 100 : 1",
      bf < 1 & bf >= .01 ~ paste("BF01 = ", round(1 / bf, k), ": 1"),
      bf >= 1 & bf < 100 ~ paste("BF01 = ", round(bf, k), ": 1"),
      bf >= 100 & bf < 1000 ~ "BF10 >= 100 : 1",
      bf >= 1000 & bf < 1000000 ~ "BF10 >= 1,000 : 1",
      bf >= 1000000 ~ "BF10 >= 1,000,000 : 1"
    ))


  if (display_type == "support") {
    results <- mutate(results, p.value = support)
  } else if (display_type == "log") {
    results <- mutate(results, p.value = logged)
  } else if (display_type == "human") {
    results <- mutate(results, p.value = human)
  } else {
    results <- mutate(results, p.value = bf)
  }
  return(results)
}

# pairwise_bf(incomedata$employment, incomedata$rint_income)
comp.list2 <- comparisons_list(incomedata, empcategory)
theme_set(hrbrthemes::theme_ipsum())

Using the employment factor in the original dataset has been useful so far. Having 7 levels has allowed us to make sure that the functions supported lots of comparisons. The downside is the resulting plots have an overwhelming amount of information. So let’s shift over to the variable empcategory which collapses employment to just 3 levels. We’ll be comparing the self-employed, to those employed in the private sector, to those employed in local, state or federal jobs.

Seems reasonable to believe that the income levels across those broad categories, might be different. I don’t have any strong prior beliefs or information before this data. It’s not an area I study or have a lot of prior information amount. Clearly, it’s out there, the ACS survey has been running for years, but for now I’m perfectly happy to say my priors are flat.

What we’re going to do:

1. Show all the possible pairwise comparisons for empcategory as bayes factors in ggplot (we’ve already built the list above in comp.list2)

2. Change the theme just to make the plots nicer theme_set(hrbrthemes::theme_ipsum())

3. Apply the ttestBF test from the BayesFactor package to the data piped into ggplot. We’ll compare income (the original untransformed data), rint_income which is our rank inverse transformed variant, and rank_income which is the income data with a simple rank transformation. N.B. - I’ve expressed the ranks so they are directionally equivalent to the raw data so the highest recorded income in our data is $250,000 which corresponds to rank of 22226.5 and after inverse transformation = 3.20299

4. Display the BF₁₀ and/or BF₀₁ values that are between 1 and 100 as is (rounded to 2 digits) and then create ranges between 100 to 1,000, 1,000 to one million and greater than one million. At some point talking about odds over 100:1 (in my humble opinion) loses the need for precision. After all is there really much difference between odds of 1,000:1 versus 1,001:1?

5. Since this post is very much about mean() versus median() both of them are plotted on top of the violin geom. The mean is displayed as a black box and the median is displayed as a dark red circle.

## Warning: `fun.y` is deprecated. Use `fun` instead.

## Warning: `fun.y` is deprecated. Use `fun` instead.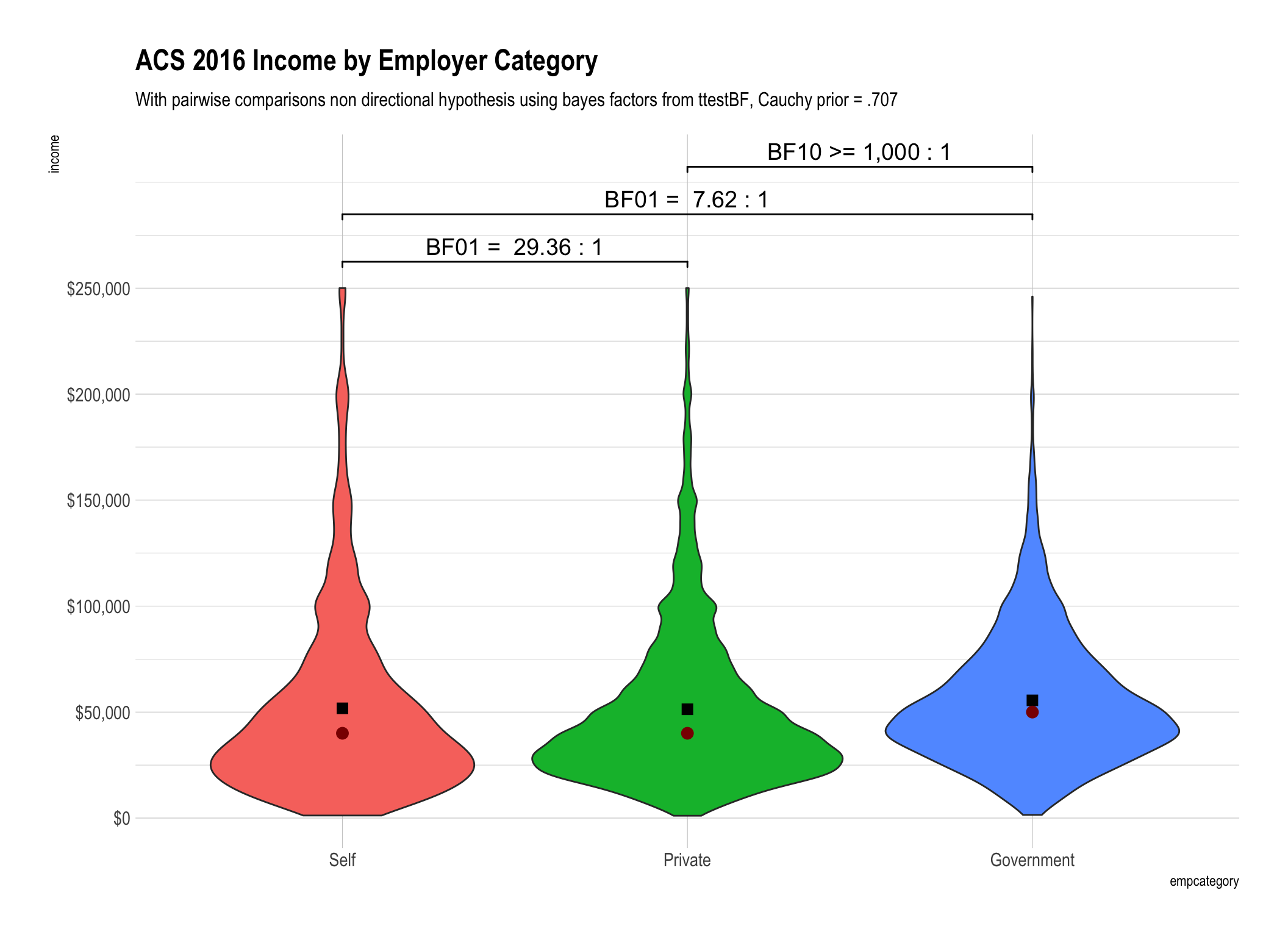

## Warning: `fun.y` is deprecated. Use `fun` instead.

## Warning: `fun.y` is deprecated. Use `fun` instead.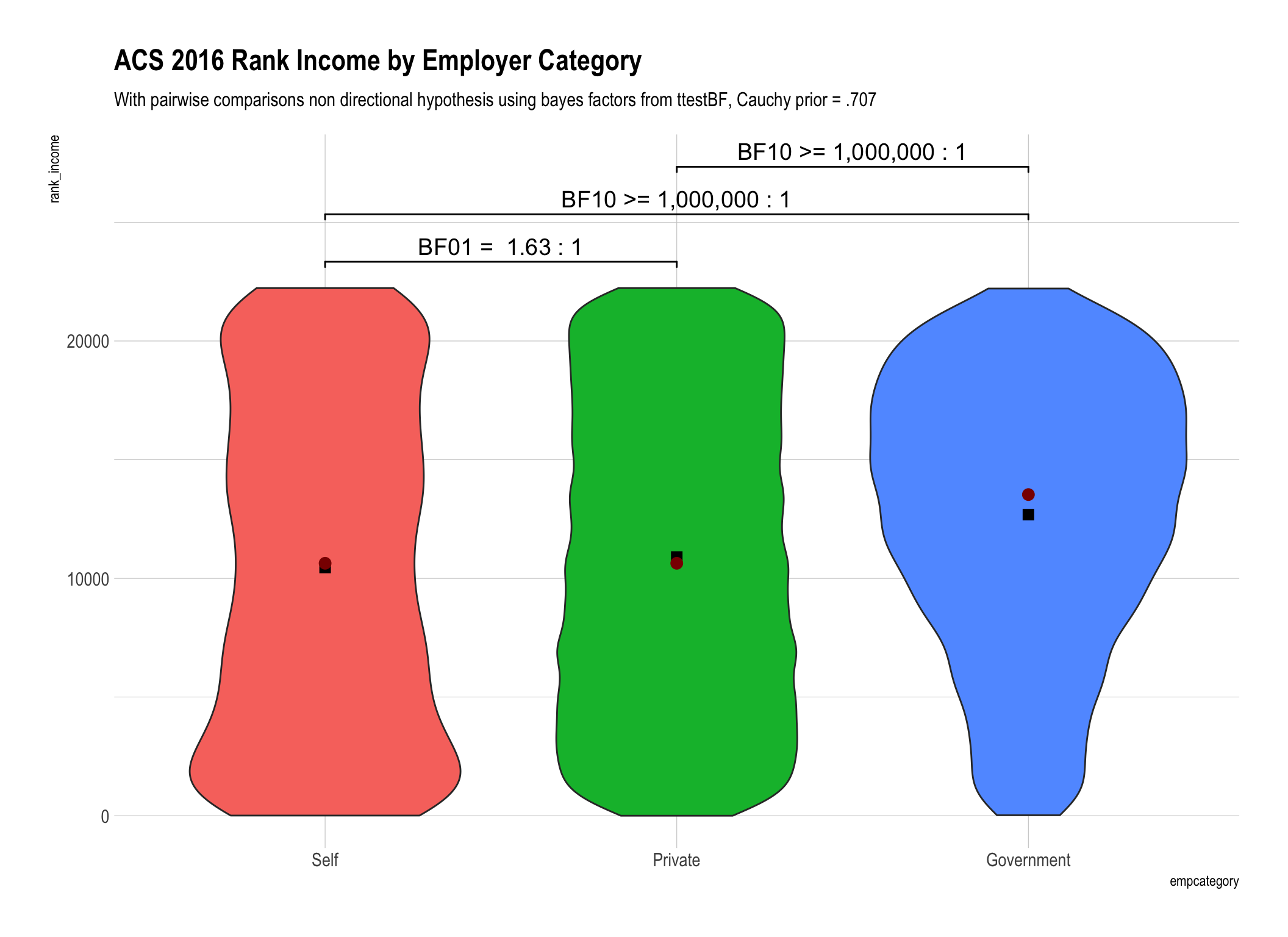

## Warning: `fun.y` is deprecated. Use `fun` instead.

## Warning: `fun.y` is deprecated. Use `fun` instead.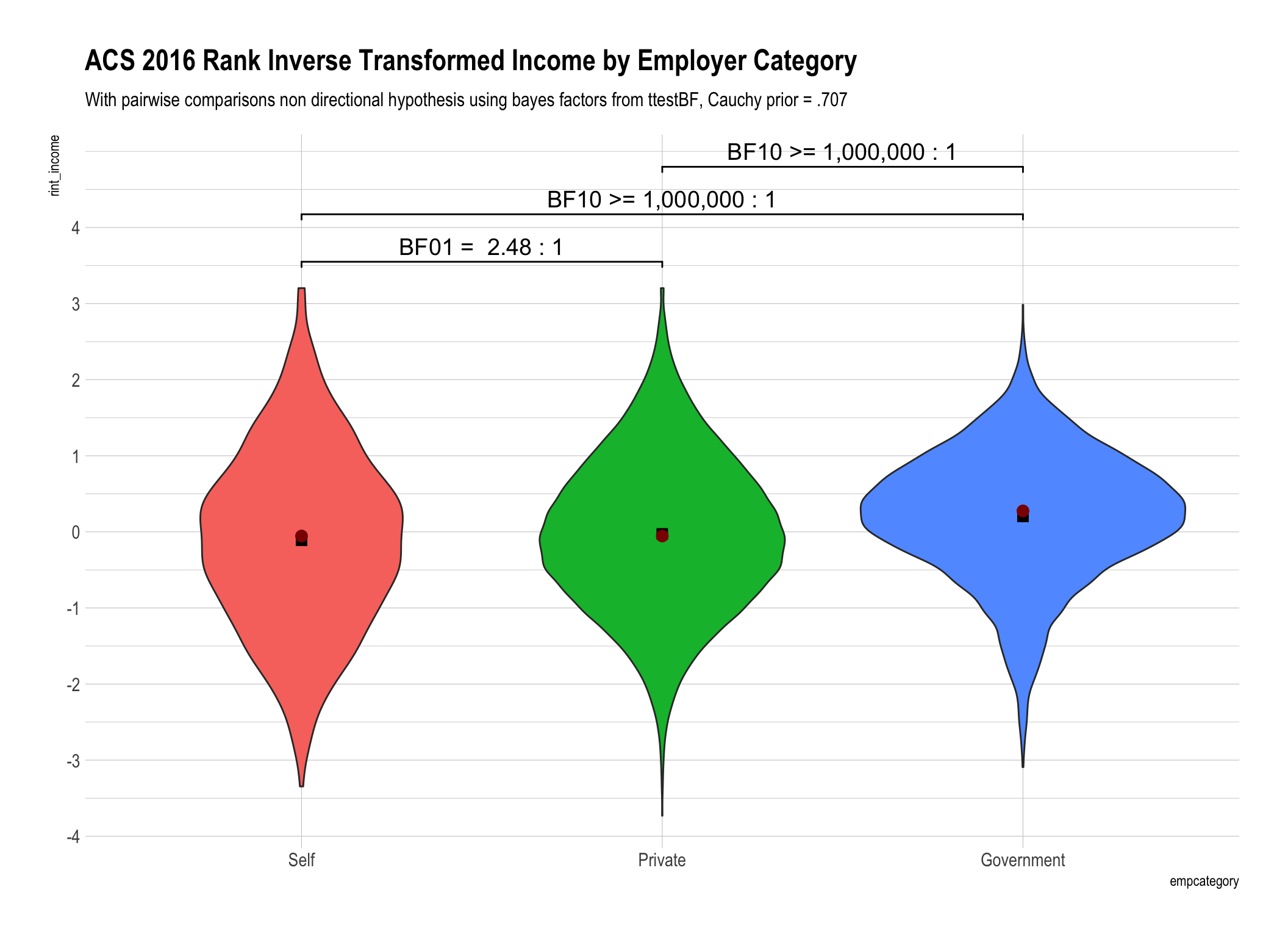

Caveat Emptor

Before I draw any conclusions about the results a reminder. While the data are “real” drawn from the U.S. Census Bureau they most assuredly are not totally representative of the entire U.S. population! The very fact that the max value for income is $250,000 tells us that this isn’t everyone and I’m not sure at all how “representative” it is. Please don’t stray from my desire to investigate the statistical properties of the methods to think I’m trying to convince you of some conclusion about the income levels of Americans.

Conclusions we can draw.

1. Distributions matter! There is a difference between investigating the mean() and the median() income and using bayesian methods doesn’t change that.

2. Bayes factors give us information in both directions! When you look at the first plot using the mean for untransformed income values BF₀₁ = 29.36 tells you that the evidence is “strong” that the mean income for the self-employed is the same as those in the private sector.

3. Whether we use simple rank transformation or reverse inverse transformed ranks our overall conclusions are similar. We have weaker “anecdotal” evidence that there is no difference between the self-employed and those in the private sector. To say it differently we are less convinced from our data that there is no difference. On the other hand we have beyond very strong evidence that government employee income is different than either the self employed or those in the private sector.

4. The difference in the bayes factors generated by using ranks versus rank inverse transformation for our data were not substantively important in magnitude. Yes they were different, for example 1.63 versus 2.48, but don’t lead us to any practically different conclusions.

5. Not withstanding #4 above until there is a “true” equivalent to the Mann Whitney for bayesian analysis I personally am far more comfortable applying a “t-test” like analysis to the data distribution that results from RINT.

Let’s get credible

I know this post is already pretty long but I promised myself I’d capture what I learned about generating credible intervals as part of this workflow. I had been asked the question by a reader I did the work and posted it in a comment but now is my chance to capture it more formally.

In my usual fashion I’m not going to try and explain the concept of a credible interval in general when others have done so already and probably done a better job. So if you’re unfamiliar with the concept I recommend a trip to Wikipedia to read up. A simple Google search will also yield lots of informative answers.

What I will focus on for the remainder of this post is simply helping you with the mechanics of constructing credible intervals if you have been following this series of posts.

So far we have been making heavy use of BayesFactor::ttestBF to accomplish our objectives. For example continuing with our last example our plot says the difference between the mean income for the privately employed and government workers is “BF10 >= 1,000:1”. We got that nice neat answer as a result of:

library(bayestestR)
tempdf <- incomedata %>%
  filter(empcategory == "Private" | empcategory == "Government") %>%
  droplevels %>%
  as.data.frame
ttestBF(formula = income ~ empcategory, data = tempdf)

## Bayes factor analysis
## --------------
## [1] Alt., r=0.707 : 357043.1 ±0%
## 
## Against denominator:
##   Null, mu1-mu2 = 0 
## ---
## Bayes factor type: BFindepSample, JZS

There it is – 357,043:1 to be more precise. And note the part that says “Null, mu1-mu2 = 0”. That looks familiar that’s a t test alright it is the difference between the means = 0. So let’s take the output from that ttestBF and but it in an object called bf.object. Sadly it’s a rather complex S4 object that doesn’t contain exactly what we need so a little more work is required. What we need to do is run some Markov chain Monte Carlo methods to sample from the posterior distribution to get our answer. While that sounds wickedly complex the function we need is built right into BayesFactor as posterior so one line does the trick posterior.data <- posterior(bf.object, iterations = 10000). What’s in posterior.data? About 10,000 rows so let’s head it.

The first column mu is the overall mean, the second column beta (Private - Government) is exactly what we need to work on it’s the difference in means “mu1-mu2” between Private and Government. The sign tells us that at least for the first 7 rows Government is higher which agrees with our plot. I have no desire to scroll through 10,000 rows so let’s get some summary information and even a plot of our 10,000 samples.

bf.object <- ttestBF(formula = income ~ empcategory, data = tempdf)
posterior.data <- posterior(bf.object, iterations = 10000)
head(posterior.data)

## Markov Chain Monte Carlo (MCMC) output:
## Start = 1 
## End = 7 
## Thinning interval = 1 
##            mu beta (Private - Government)       sig2       delta         g
## [1,] 53561.49                   -4038.896 1395801266 -0.10810628 0.1494593
## [2,] 53212.31                   -4068.549 1404665553 -0.10855581 6.9421183
## [3,] 53596.74                   -4163.078 1375094603 -0.11226601 0.1244661
## [4,] 53946.27                   -4641.400 1394097484 -0.12430897 0.2774587
## [5,] 53787.24                   -3764.657 1387330824 -0.10107304 0.3187737
## [6,] 53224.95                   -3615.114 1412016885 -0.09620598 0.2283490
## [7,] 53109.83                   -2832.885 1378115193 -0.07631084 0.8811414

summary(posterior.data)

## 
## Iterations = 1:10000
## Thinning interval = 1 
## Number of chains = 1 
## Sample size per chain = 10000 
## 
## 1. Empirical mean and standard deviation for each variable,
##    plus standard error of the mean:
## 
##                                   Mean        SD  Naive SE Time-series SE
## mu                           5.342e+04 3.691e+02 3.691e+00      6.374e+00
## beta (Private - Government) -4.185e+03 7.346e+02 7.346e+00      1.289e+01
## sig2                         1.395e+09 1.367e+07 1.367e+05      1.367e+05
## delta                       -1.120e-01 1.967e-02 1.967e-04      3.448e-04
## g                            2.364e+00 2.590e+01 2.590e-01      3.012e-01
## 
## 2. Quantiles for each variable:
## 
##                                   2.5%        25%        50%        75%
## mu                           5.269e+04  5.317e+04  5.343e+04  5.367e+04
## beta (Private - Government) -5.642e+03 -4.673e+03 -4.181e+03 -3.702e+03
## sig2                         1.369e+09  1.386e+09  1.395e+09  1.405e+09
## delta                       -1.510e-01 -1.250e-01 -1.119e-01 -9.909e-02
## g                            6.932e-02  1.902e-01  3.773e-01  9.108e-01
##                                  97.5%
## mu                           5.414e+04
## beta (Private - Government) -2.740e+03
## sig2                         1.422e+09
## delta                       -7.325e-02
## g                            1.039e+01

plot(posterior.data[,"beta (Private - Government)"])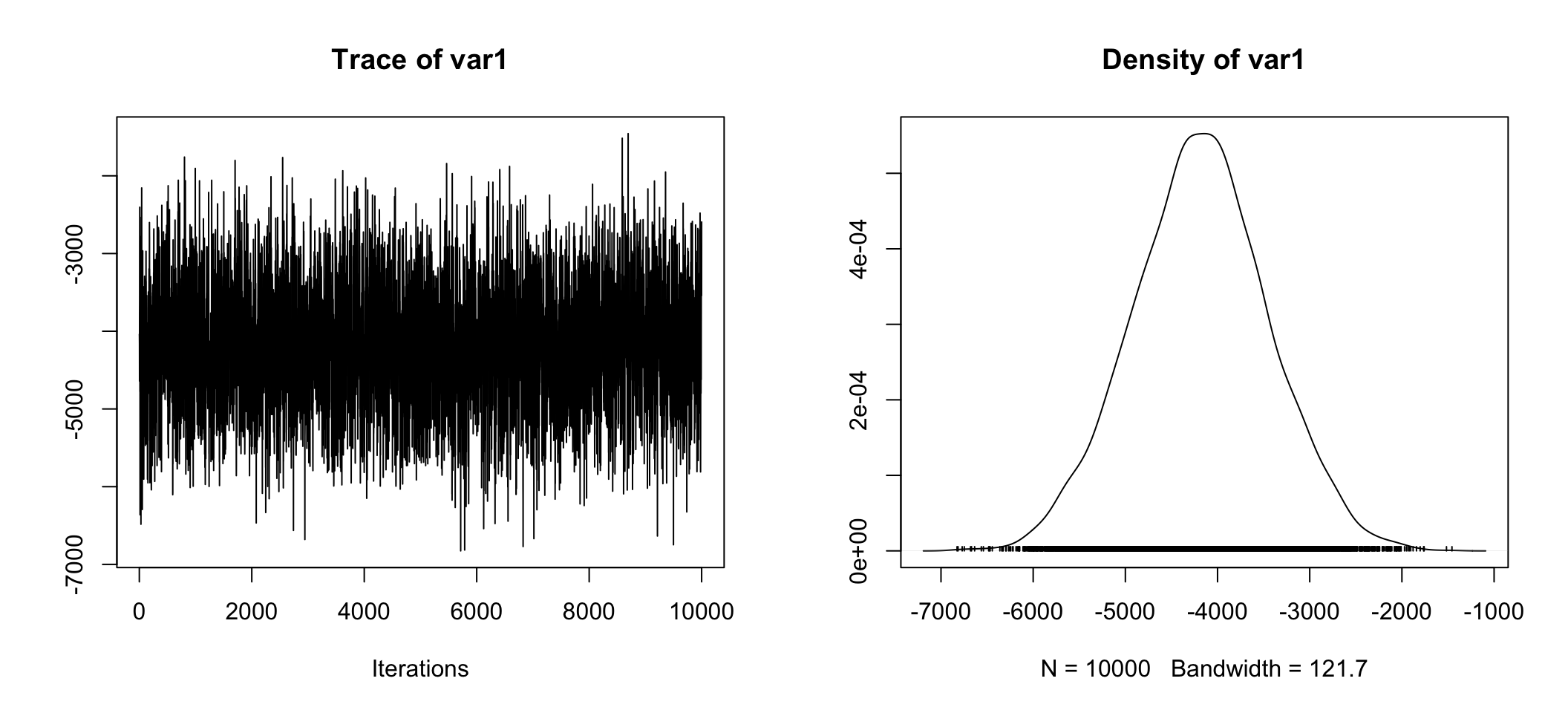

Whether we look at the right hand plot, or the tabular information Mean = -4.188e+03, 50% = -4.182e+03, sure looks like the difference estimate is about ~ -$4,180. Also telling is 2.5% = -5.615e+03 and 97.5% = -2.775e+03 which means 95% of our estimates were between -$5,615 and -$2,775! Anyone care to guess what the 95% credible interval is?

Well of course we don’t have to guess. We can take our posterior.data object and change it to a dataframe. After we’ve done that we can use bayestestR::ci (you may have noticed I loaded the library a few lines back). And there you have it the 89% credible interval is [-5352.79, -3042.40]. Wait. What? 89%????

posterior.data <- as.data.frame(posterior.data)
str(posterior.data)

## 'data.frame':    10000 obs. of  5 variables:
##  $ mu                         : num  53561 53212 53597 53946 53787 ...
##  $ beta (Private - Government): num  -4039 -4069 -4163 -4641 -3765 ...
##  $ sig2                       : num  1.40e+09 1.40e+09 1.38e+09 1.39e+09 1.39e+09 ...
##  $ delta                      : num  -0.108 -0.109 -0.112 -0.124 -0.101 ...
##  $ g                          : num  0.149 6.942 0.124 0.277 0.319 ...

bayestestR::ci(posterior.data$`beta (Private - Government)`)

## # Equal-Tailed Interval
## 
## 89% ETI             
## --------------------
## [-5370.74, -2998.33]

For an explanation of why please see the bayestestR documentation. While you’re there good chance to review what a credible interval is, how it is interpreted, and our next topic which is that there are at least two equally valid ways of computing it. The first we used already it’s the Equal-tailed Interval (ETI) which is the default when you invoke ci. The other is Highest Density Interval (HDI) hdi(). They do a good job of explaining so I won’t repeat merely show you how.

ci() will accept a vector with multiple cut-offs so let’s do 89% and 95% once with equal-tailed and then with highest density. To be fair at least for the equal tailed you can use base R’s quantile function to get the same answers. BTW back a little bit when we were looking at summary(posterior.data) the answer for 95% was right there just hard to pick out.

ci(posterior.data$`beta (Private - Government)`, 
   ci = c(.89, .95))

## # Equal-Tailed Intervals
## 
## 89% ETI             
## --------------------
## [-5370.74, -2998.33]
## 
## 
## 95% ETI             
## --------------------
## [-5641.72, -2740.31]

hdi(posterior.data$`beta (Private - Government)`, 
    ci = c(.89, .95))

## # Highest Density Intervals
## 
## 89% HDI             
## --------------------
## [-5371.36, -3002.55]
## 
## 
## 95% HDI             
## --------------------
## [-5629.60, -2729.79]

round(quantile(posterior.data$`beta (Private - Government)`, 
         probs = c(.025, 
                   .055, 
                   (1 - .055), 
                   (1 - .025)
                   )
         ), 
      2)

##     2.5%     5.5%    94.5%    97.5% 
## -5641.72 -5370.74 -2998.33 -2740.31

So given our observed data, the mean difference in income between the private sector respondents and the government employed respondents has a 95% probability of falling between -$5,614.99 and -$2,774.84.

We can preform the exact same operations on rint_income if we want to convince ourselves that the mean difference (which for rint_income is more akin to the median difference) is not equal to zero). The problem of course is that it doesn’t return a dollar value and our transformations are non-linear.

bf.object <- ttestBF(formula = rint_income ~ empcategory, data = tempdf)
posterior.data <- posterior(bf.object, iterations = 10000)
summary(posterior.data)

## 
## Iterations = 1:10000
## Thinning interval = 1 
## Number of chains = 1 
## Sample size per chain = 10000 
## 
## 1. Empirical mean and standard deviation for each variable,
##    plus standard error of the mean:
## 
##                                 Mean        SD  Naive SE Time-series SE
## mu                           0.08814  0.009554 9.554e-05      1.612e-04
## beta (Private - Government) -0.22957  0.019015 1.901e-04      3.191e-04
## sig2                         0.96654  0.009428 9.428e-05      9.428e-05
## delta                       -0.23352  0.019378 1.938e-04      3.248e-04
## g                            2.06437 20.075695 2.008e-01      2.008e-01
## 
## 2. Quantiles for each variable:
## 
##                                 2.5%     25%      50%     75%   97.5%
## mu                           0.06976  0.0815  0.08792  0.0947  0.1071
## beta (Private - Government) -0.26716 -0.2425 -0.22939 -0.2165 -0.1926
## sig2                         0.94833  0.9601  0.96653  0.9728  0.9851
## delta                       -0.27228 -0.2467 -0.23335 -0.2203 -0.1960
## g                            0.07624  0.2006  0.39943  0.9836 10.5321

plot(posterior.data[,"beta (Private - Government)"])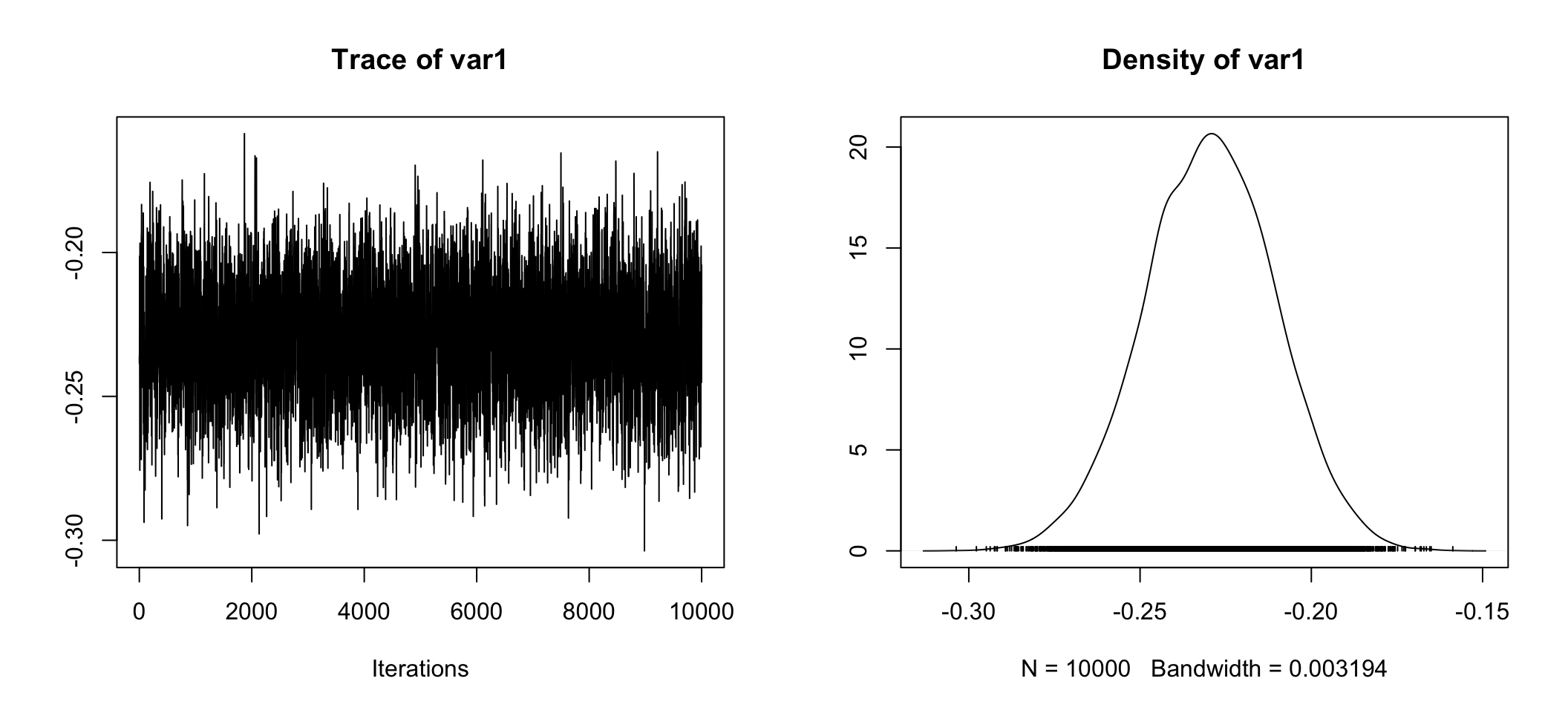

posterior.data <- as.data.frame(posterior.data)
bayestestR::ci(posterior.data$`beta (Private - Government)`)

## # Equal-Tailed Interval
## 
## 89% ETI       
## --------------
## [-0.26, -0.20]

ci(posterior.data$`beta (Private - Government)`, 
   ci = c(.89, .95))

## # Equal-Tailed Intervals
## 
## 89% ETI       
## --------------
## [-0.26, -0.20]
## 
## 
## 95% ETI       
## --------------
## [-0.27, -0.19]

hdi(posterior.data$`beta (Private - Government)`, 
    ci = c(.89, .95))

## # Highest Density Intervals
## 
## 89% HDI       
## --------------
## [-0.26, -0.20]
## 
## 
## 95% HDI       
## --------------
## [-0.27, -0.19]

A final look at why it matters

So I wanted to end this post by reinforcing why mean() vs median() matters. Continuing to focus on the differences between income in the private sector and government employees remember we saw the BF associated with the difference between the two groups increase an order of magnitude when we shifted from assessing mean differences to median differences. Why?

Well take a look at the differences expressed in the original dollar units. The mean difference is about ~$4,200, the median difference is more than twice as much at ~$10,000, that’s a big difference.

psych::describeBy(incomedata$income, 
                  group = incomedata$empcategory, 
                  mat = TRUE, 
                  digits = 2) %>%
  mutate(.data = ., 
         Employment_Type = group1,
         trimmed_mean = trimmed) %>%
  select(Employment_Type, 
         mean, 
         sd,
         median, 
         skew,
         n,
         trimmed_mean)

##   Employment_Type     mean       sd median skew     n trimmed_mean
## 1            Self 51771.00 44154.93  40000 1.82  1398     44342.71
## 2         Private 51326.42 38381.11  40000 1.82 17743     45221.13
## 3      Government 55521.62 30830.33  50000 1.28  3100     52263.65

a <- median(incomedata[incomedata$empcategory == "Private", "income"])
b <- median(incomedata[incomedata$empcategory == "Government", "income"])
c <- mean(incomedata[incomedata$empcategory == "Private", "income"])
d <- mean(incomedata[incomedata$empcategory == "Government", "income"])

median_diff_priv_govt <- a - b
median_diff_priv_govt

## [1] -10000

mean_diff_priv_govt <- c - d
mean_diff_priv_govt

## [1] -4195.196

For a final plot we’ll show it in the original units and then to make it easier to see give you a zoomed perspective with coord_cartesian(). The dashed lines are the median values by group (which are color-coded) and the solid lines are the mean.

tempdf %>%
  ggplot(aes(x = income, 
             fill = empcategory,
             color = empcategory)
         ) +
  geom_density(alpha = .3) +
  geom_vline(xintercept = a, linetype = 5, color = "coral1") +
  geom_vline(xintercept = b, linetype = 5, color = "cyan3") +
  geom_vline(xintercept = c, color = "coral1") +
  geom_vline(xintercept = d, color = "cyan3") +
  scale_x_continuous(label = dollar)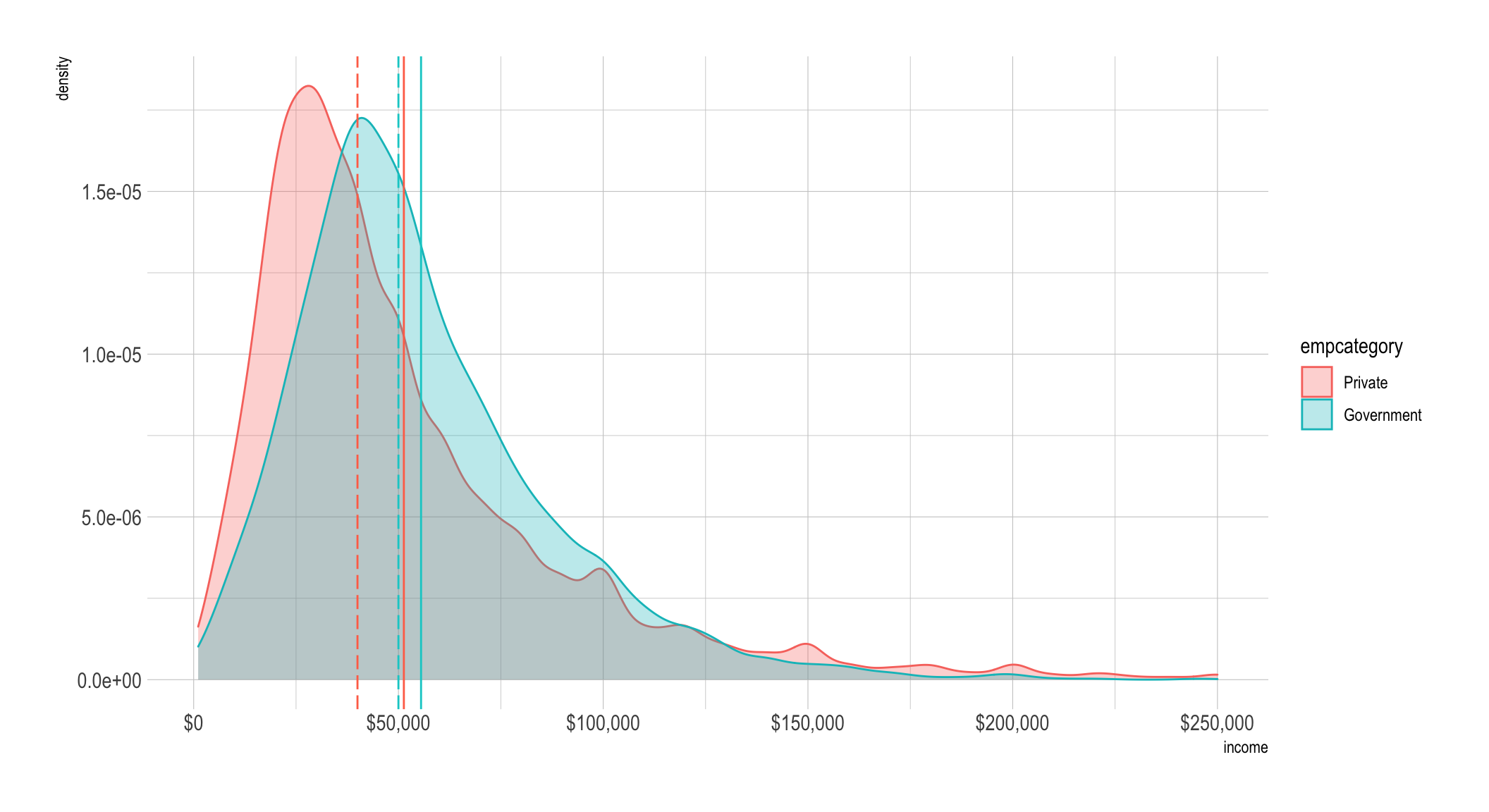

tempdf %>%
  ggplot(aes(x = income, 
             fill = empcategory,
             color = empcategory)
         ) +
  geom_density(alpha = .3) +
  geom_vline(xintercept = a, linetype = 5, color = "coral1") +
  geom_vline(xintercept = b, linetype = 5, color = "cyan3") +
  geom_vline(xintercept = c, color = "coral1") +
  geom_vline(xintercept = d, color = "cyan3") +
  scale_x_continuous(label = dollar) +
  coord_cartesian(xlim = c(10000, 100000))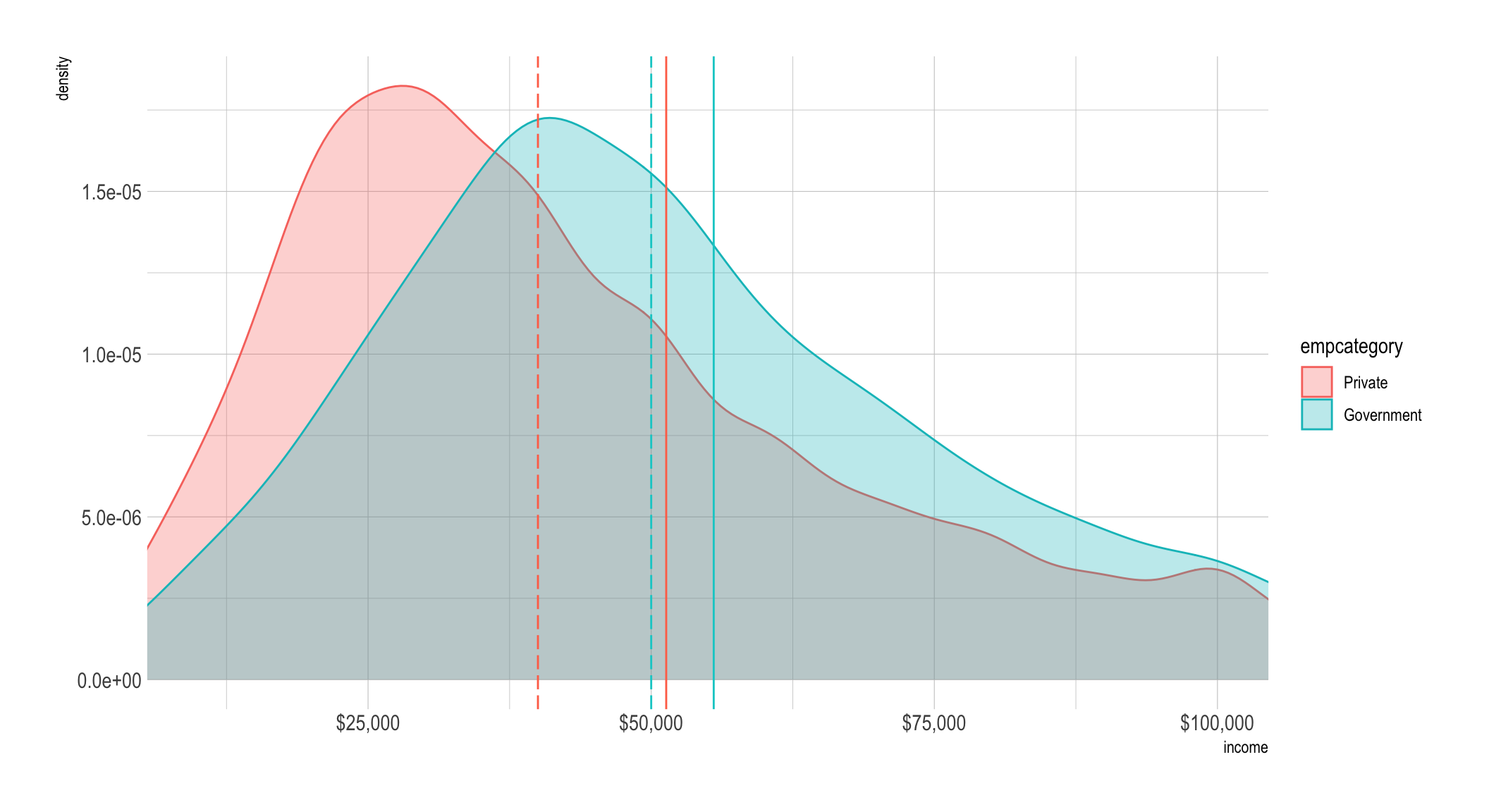

Done

Hope you enjoyed the post. Comments always welcomed.

Chuck

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License