ANCOVA Example
Analysis of covariance (ANCOVA) using R.
I recently had the need to run an ANCOVA, not a task I perform all that often
and my first time using R to do so (I’ve done it in SPSS and SAS before).
Having a decent theoretical idea of what I had to do I set of in search of
decent documentation of how to accomplish it in R. I was quite disappointed with
what I found after a decent amount of time scouring the web (or at least I
thought so). I found “answers” in places like Stack Overflow" and “Cross
Validated” as well as various free and open notes from academic courses. Many
were dated, a few off topic, a few outright incorrect if you ask me but nothing
I could just pick up and use.
So I wrote my own top to bottom example that I’ll publish on my blog not necessarily because others will find it but more to ensure I document my own learning. I may also cross post a shortened version in a couple of places and point back to this longish posting.
Before you read any farther
Some constraints I’m placing on this post that may impact your desire to read it.
- Yes ANOVA is a subset of the general linear model and specifically in R
aovis just a wrapper aroundlm. I can’t tell you the number of times I read that and it’s true. But, in many disciplines and for me it is an important subset worthy of it’s own time. You won’t find any info here about how to do things withlmalthough you certainly could. - Yes contrasts can play an important role in understanding your results. This is especially true if you happen to have an unbalanced design. I’m only going to glance on the topic here since I’m going to run a balanced design and therefore contrasts are tangential. For a very good academic discussion of contrasts especially using R and especially at the introductory level I very strongly recommend Learning Statistics with R, (search and ye shall find) where Danielle has done a great job of covering the topic in several places. The text is free for the download and is invaluable although it doesn’t cover ANCOVA per se.
- I’m going to use packages above and beyond
baseandstatsas needed. Everything could be done with the basics but this is a practical approach not so much a theoretical approach. I’ll even put in a very subtle plug for a function I wrote and maintain onCRANalthough it’s by no means required.
N.B. - I don’t expect this will reach the New York Times best-seller list but questions or comments if it useful or if I have missed something are most certainly welcome.
Background and problem statement
The Wikipedia definition of
ANCOVA is actually quite
good and I won’t bother to repeat it. Some other keys phrases you’ll hear are
that ANCOVA allows you to “control for” or “partial out” the covariate which
gives you the opportunity to estimate partial means or marginal means which
at the end of the day is why one uses ANOVA/ANCOVA versus regression. They use
the same math but ANOVA/ANCOVA typically reports in means and mean differences
while regressions reports on the slopes of the regression terms. Yes you can
move back and forth but many disciplines have a preference and it can be one
less step.
I wanted to make sure I used a dataset that was easily accessible. I mean that
both in terms of being available in a package that most users will all ready
have as well on a topic that many will find intuitively understandable with no
specialized knowledge. I selected the diamonds dataset from ggplot2. I’ll
cut it down some and balance it but those are trivial steps that will hopefully
make things clearer.
So imagine that you’re shopping for a diamond. You’d like to get the possible
value for the money you spend but you have very little knowledge about what
influences the price you pay versus the value you get. The sales people speak
about various things that influence the price such as “cut” and “clarity” and
“color” and “carats”. You don’t have a lot to spend so you’re going to limit
yourself to something modest but you’d like to know you got good value for what
you paid. Enter the diamond dataset from ggplot2 if you have library
available you can get a terse description with ?diamonds.
Let’s say for the sake of argument you’d like to know more about how these
factors of cut and color impact the price you’ll pay. Let’s go ahead and
get things set up in R so we can proceed, load the right libraries etc..
You’ll see in the code I recommend grabbing the latest version of a package I
maintain but it is totally optional and there’s nothing there you can’t do for
yourself if you prefer. I just wrote it so I didn’t have to remember to repeat a
bunch of steps in R to run a 2Way ANOVA. You can see the docs
here.
I’m going to assume you’re comfortable with a basic ANOVA although you’re
welcome to review the vignette if that’s helpful. So let’s load the libraries (I’ve
suppressed all the messages here), and check out the structure of the dataset.
require(car) # get the right sums of squares calculations
require(dplyr) # for manipulating our data
require(ggplot2) # for plotting and for our dataset
require(sjstats) # save us time computing key ANOVA stats beyond car
require(broom) # nice for making our results in neat tibbles
require(emmeans) # for marginal means calculations
# a shameless plug for a function I wrote called Plot2WayANOVA
# optional for you
# devtools::install_github("ibecav/CGPfunctions")
library(CGPfunctions)
theme_set(theme_bw()) # set theme
str(diamonds)## tibble [53,940 × 10] (S3: tbl_df/tbl/data.frame)
## $ carat : num [1:53940] 0.23 0.21 0.23 0.29 0.31 0.24 0.24 0.26 0.22 0.23 ...
## $ cut : Ord.factor w/ 5 levels "Fair"<"Good"<..: 5 4 2 4 2 3 3 3 1 3 ...
## $ color : Ord.factor w/ 7 levels "D"<"E"<"F"<"G"<..: 2 2 2 6 7 7 6 5 2 5 ...
## $ clarity: Ord.factor w/ 8 levels "I1"<"SI2"<"SI1"<..: 2 3 5 4 2 6 7 3 4 5 ...
## $ depth : num [1:53940] 61.5 59.8 56.9 62.4 63.3 62.8 62.3 61.9 65.1 59.4 ...
## $ table : num [1:53940] 55 61 65 58 58 57 57 55 61 61 ...
## $ price : int [1:53940] 326 326 327 334 335 336 336 337 337 338 ...
## $ x : num [1:53940] 3.95 3.89 4.05 4.2 4.34 3.94 3.95 4.07 3.87 4 ...
## $ y : num [1:53940] 3.98 3.84 4.07 4.23 4.35 3.96 3.98 4.11 3.78 4.05 ...
## $ z : num [1:53940] 2.43 2.31 2.31 2.63 2.75 2.48 2.47 2.53 2.49 2.39 ...Okay just crossing cut and color would give us 35 cells in a table of means
( 5 levels times 7 levels). I’ve also admitted I’m a cheapskate and don’t want a
huge diamond so let’s pare our data down a bit to something more manageable. So
let’s use dplyr to create a subset of the data where we focus on “fair” and
“good” cuts, and colors “E”, “F”, and “G” with a carat weight of less than 1.75.
This is also a good time to admit I cheated and peeked and saw that the data
were likely to be very unbalanced table(diamonds$color, diamonds$cut), so at
this point I’m also going to force our data into a balanced design by ensuring
that we randomly sample the same number of data points into each cell. I’ve used
set.seed so you should be able to reproduce the same dataset if you choose.
set.seed(1234)
diamonds2 <- filter(diamonds,
cut %in% c("Fair", "Good") &
color %in% c("E", "F", "G") &
carat < 1.75)
diamonds2 <- droplevels(diamonds2)
one <- diamonds2 %>% filter(cut == "Fair" & color == "E") %>% sample_n(218)
two <- diamonds2 %>% filter(cut == "Fair" & color == "F") %>% sample_n(218)
three <- diamonds2 %>% filter(cut == "Fair" & color == "G") %>% sample_n(218)
four <- diamonds2 %>% filter(cut == "Good" & color == "E") %>% sample_n(218)
five <- diamonds2 %>% filter(cut == "Good" & color == "F") %>% sample_n(218)
six <- diamonds2 %>% filter(cut == "Good" & color == "G") %>% sample_n(218)
diamonds2 <- bind_rows(one, two, three, four, five, six)
str(diamonds2)## tibble [1,308 × 10] (S3: tbl_df/tbl/data.frame)
## $ carat : num [1:1308] 0.92 1.01 0.5 1.32 1 0.5 0.31 0.51 0.34 0.4 ...
## $ cut : Ord.factor w/ 2 levels "Fair"<"Good": 1 1 1 1 1 1 1 1 1 1 ...
## $ color : Ord.factor w/ 3 levels "E"<"F"<"G": 1 1 1 1 1 1 1 1 1 1 ...
## $ clarity: Ord.factor w/ 8 levels "I1"<"SI2"<"SI1"<..: 3 3 3 2 6 2 4 3 7 4 ...
## $ depth : num [1:1308] 65.6 65.3 66.5 65.2 65.4 58 54.2 55.8 54 64.7 ...
## $ table : num [1:1308] 57 59 58 58 56 67 63 61 56 58 ...
## $ price : int [1:1308] 3407 4844 1098 6221 7918 851 814 1340 1012 813 ...
## $ x : num [1:1308] 6.1 6.13 4.87 6.86 6.28 5.26 4.61 5.43 4.8 4.63 ...
## $ y : num [1:1308] 6.07 6.19 4.9 6.79 6.2 5.17 4.51 5.35 4.76 4.67 ...
## $ z : num [1:1308] 3.99 4.02 3.25 4.45 4.08 3.02 2.47 3.01 2.58 3.01 ...A note on balanced designs
As I noted earlier I’m really not interested in digressing to talk about why the
concept of a balanced design is important to your work. Please do consult
Learning Statistics with R for more
details. At this point I’m simply going to encourage you to always use “Type II”
sums of squares from the car package if there is any chance your design is
unbalanced. If your design is balanced they give the same answer. The contrast
you choose is also if you are unbalanced and are using Type III.
Are unbalanced designs completely wrong and to be avoided at all costs? Not exactly… here are three things they impact in order of likelihood.
- They always impact your power, you ability to detect significant differences. Your power is limited by the size of your smallest cell.
- They usually impact your ability to divide the sums of squares cleanly to 100%. You may wind up with unexplained variance that is due to an effect but you won’t which effect. This is different than unexplained (residual variance).
- The least likely but most worrisome is that it will mask an important relationship in your data.
Back to the diamonds
Before we look at ANCOVA lets run an ANOVA. We have two ordinal factors for
independent (predictor) variables cut and color and one dependent (outcome)
variable the price. A classic two-way ANOVA. We could simply run `aov(price ~
cut * color, diamonds2) and then a bunch of other commands to get the
information we need. I found that a bit tedious and annoying plus I wanted to be
able to plot the results to look at any possible interactions. So I wrote a
function. Everything in it you can do by hand but I think it does a pretty good
job wrapping the process in one function. So …
Plot2WayANOVA(price ~ color * cut,
diamonds2,
mean.label = TRUE)##
## You have a balanced design.## term sumsq meansq df statistic p.value etasq
## color color 4.807090e+06 2403545.03 2 0.325 0.722 0.000
## cut cut 1.235500e+02 123.55 1 0.000 0.997 0.000
## color:cut color:cut 7.664167e+06 3832083.61 2 0.519 0.595 0.001
## ...4 Residuals 9.614813e+09 7384649.03 1302 NA NA NA
## partial.etasq omegasq partial.omegasq epsilonsq cohens.f power
## color 0.000 -0.001 -0.001 -0.001 0.022 0.102
## cut 0.000 -0.001 -0.001 -0.001 0.000 0.050
## color:cut 0.001 -0.001 -0.001 -0.001 0.028 0.136
## ...4 NA NA NA NA NA NA##
## Table of group means## # A tibble: 6 x 15
## # Groups: color [3]
## color cut TheMean TheSD TheSEM CIMuliplier LowerBoundCI UpperBoundCI
## <ord> <ord> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 E Fair 3406. 2485. 168. 1.97 3075. 3738.
## 2 E Good 3425. 3260. 221. 1.97 2989. 3860.
## 3 F Fair 3392. 2484. 168. 1.97 3061. 3724.
## 4 F Good 3196. 2698. 183. 1.97 2836. 3556.
## 5 G Fair 3340. 2327. 158. 1.97 3030. 3651.
## 6 G Good 3517. 2940. 199. 1.97 3125. 3910.
## # … with 7 more variables: LowerBoundSEM <dbl>, UpperBoundSEM <dbl>,
## # LowerBoundSD <dbl>, UpperBoundSD <dbl>, N <int>, LowerBound <dbl>,
## # UpperBound <dbl>##
## Post hoc tests for all effects that were significant## [1] "No signfiicant effects"##
## Testing Homogeneity of Variance with Brown-Forsythe## *** Possible violation of the assumption ***## Brown-Forsythe Test for Homogeneity of Variance using median
## Df F value Pr(>F)
## group 5 3.2086 0.00695 **
## 1302
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1##
## Testing Normality Assumption with Shapiro-Wilk## *** Possible violation of the assumption. You may
## want to plot the residuals to see how they vary from normal ***##
## Shapiro-Wilk normality test
##
## data: MyAOV_residuals
## W = 0.84893, p-value < 2.2e-16##
## Bayesian analysis of models in order## # A tibble: 4 x 4
## model bf support margin_of_error
## <chr> <dbl> <chr> <dbl>
## 1 cut 0.0620 " data support is strong" 0.00170
## 2 color 0.0123 " data support is very stro… 0.0000980
## 3 color + cut 0.000730 " data support is extreme" 0.0156
## 4 color + cut + color:cut 0.0000224 " data support is extreme" 0.0647##
## Interaction graph plotted...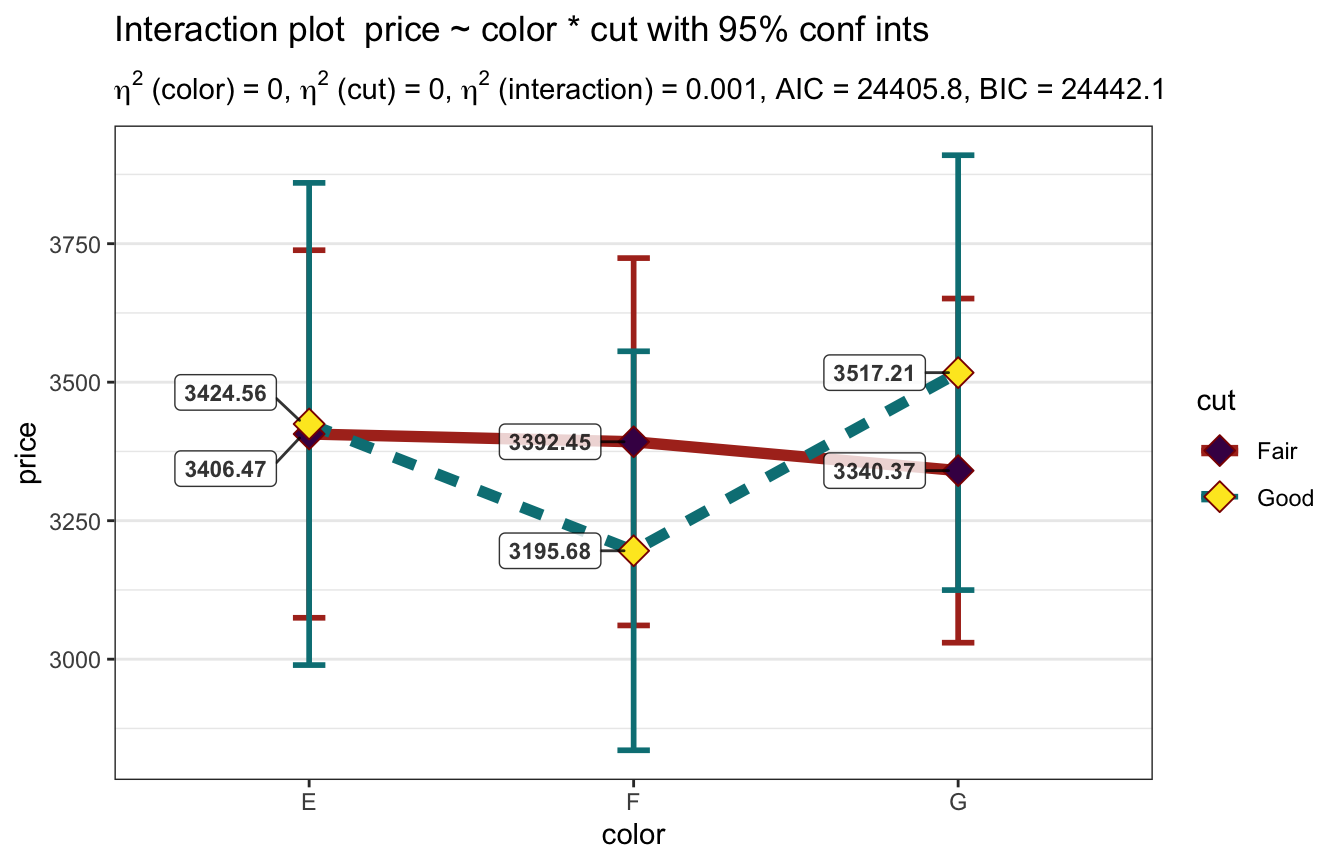
It does it’s job of plotting the results and providing you with nice summaries of not just the ANOVA table but the table of means, post hoc tests if needed and even testing classic assumptions. it also tests for whether your design is balanced and always uses type II sums of squares.
Well this is unfortunate! Looks like I won’t be publishing the results in JODR
- The Journal of Obscure Diamond Results since not a single one of my ANOVA
terms is significant at the p<.05 level. The model seems to be a terrible fit
whether I look at R Squared or AIC or BIC, neither cut nor color seem to
matter although the interaction term is “marginally significant”.
Should we conclude cut and color don’t matter? Are they just immaterial with
no discernible impact on pricing?
ANCOVA helps our understanding
As you have probably already guessed that’s not where we’re heading. Remember that Wikipedia article? A telling quote from Tabachnick, B. G. and Fidell, L. S. (2007) is in there…
ANCOVA can be used to increase statistical power (the probability a significant difference is found between groups when one exists) by reducing the within-group error variance.
So with ANCOVA we’re going to add one or more continuous variables known as
covariates which are “hiding” the relationship between our factors of interest
cut and color, if we can control for or partial the covariate out then we’ll
hopefully be likely to “see” the impact of cut and color on price. It should
be something we know is linearly related to price but distinct from cut and
color.
So looking at our data above it hopefully is becoming obvious to you. On surface
to meet the criteria of being a continuous numeric variable we have "carat",
"depth", "table", "x", "y" and "z". Since clarity is ordered we
could force it to an integer and use it but let’s not. Speaking for me, I’m
pretty sure size as measured in weight carat is going to be related to price
of the diamond. I don’t know much about diamonds but I’ve heard size adds to the
cost…
So what we want to do now is confirm our hunch it is linearly related as well as
hope that it is not strongly correlated with our current predictors cut and
color we’re looking for a variable that reduces the variance but is not
entangled with our current IVs. So first a scatter plot with the regression and
loess lines followed by a glance at the linear models price ~ carat, carat ~ cut, and carat ~ color.
ggplot(diamonds2, aes(x = carat, y= price)) +
geom_point(alpha = 1/10) +
geom_smooth(method = "loess", color = "red") +
geom_smooth(method = "lm", color = "blue")## `geom_smooth()` using formula 'y ~ x'
## `geom_smooth()` using formula 'y ~ x'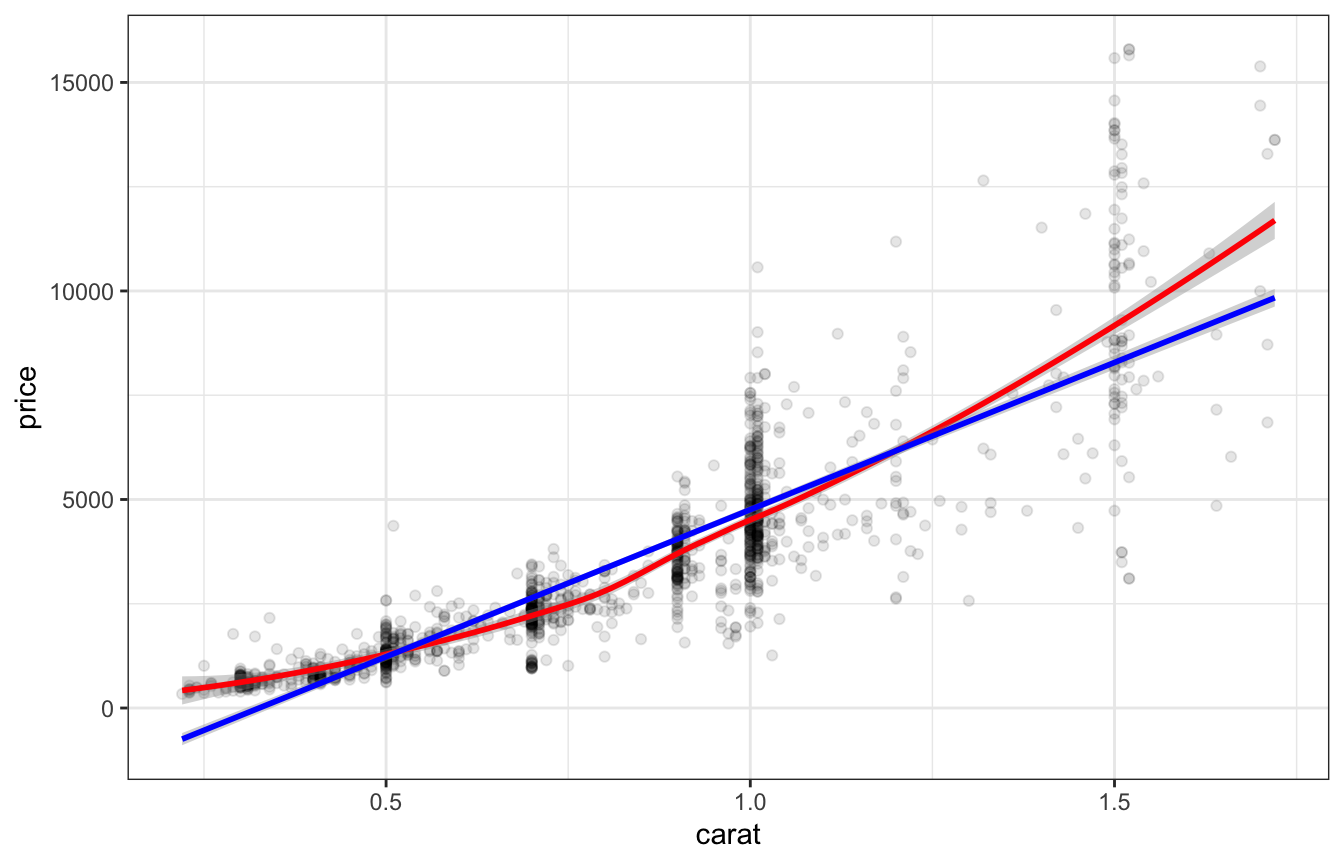
broom::glance(lm(price ~ carat, diamonds2))## # A tibble: 1 x 12
## r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 0.756 0.756 1340. 4057. 0 1 -11273. 22552. 22567.
## # … with 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>broom::glance(lm(carat ~ cut, diamonds2))## # A tibble: 1 x 12
## r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 0.0190 0.0182 0.332 25.2 5.75e-7 1 -411. 828. 843.
## # … with 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>broom::glance(lm(carat ~ color, diamonds2))## # A tibble: 1 x 12
## r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 0.00292 0.00139 0.334 1.91 0.148 2 -421. 851. 872.
## # … with 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>caratonly <- lm(price ~ carat, diamonds2)Excellent news! Our potential covariate carat is highly correlated with
price (r = 0.87) while having
near zero correlations with cut (r = 0.14) and color (r = 0.05).
Comparing models
We’re going to compare two different models in a step by step fashion using
the same tools in R for each step, aov to create the model, car::Anova to
display the ANOVA table and ensure we’re using type 2 sums of squares.
broom::glance to get information about overall fir like R squared and AIC, and
finally sjstats::anova_stats to give us a nice clean display including effect
sizes for the terms.
So our original model without a covariate looked like this (you can scroll back and look but I assure you this is it).
noCOVmodel <- aov(price ~ cut * color, diamonds2)
car::Anova(noCOVmodel, type = 2)## Anova Table (Type II tests)
##
## Response: price
## Sum Sq Df F value Pr(>F)
## cut 124 1 0.0000 0.9967
## color 4807090 2 0.3255 0.7222
## cut:color 7664167 2 0.5189 0.5953
## Residuals 9614813032 1302broom::glance(noCOVmodel)## # A tibble: 1 x 6
## logLik AIC BIC deviance nobs r.squared
## <dbl> <dbl> <dbl> <dbl> <int> <dbl>
## 1 -12196. 24406. 24442. 9614813032. 1308 0.00130sjstats::anova_stats(car::Anova(noCOVmodel, type = 2)) %>% select(1:7)## term sumsq meansq df statistic p.value etasq
## cut cut 1.235500e+02 123.55 1 0.000 0.997 0.000
## color color 4.807090e+06 2403545.03 2 0.325 0.722 0.000
## cut:color cut:color 7.664167e+06 3832083.61 2 0.519 0.595 0.001
## ...4 Residuals 9.614813e+09 7384649.03 1302 NA NA NAAdding carat to the model
Let’s add another term to the model to include carat, we’re not going to let it
interact with the other factors so we’ll use a plus sign. There’s nothing
especially tricky about this, we’re just adding another predictor to our model,
it’s not exactly traditional ANOVA because it’s a continuous numeric variable
rather than a factor, but it’s simple to imagine.
COVmodel <- aov(price ~ cut * color + carat, diamonds2)
car::Anova(COVmodel, type = 2)## Anova Table (Type II tests)
##
## Response: price
## Sum Sq Df F value Pr(>F)
## cut 141145906 1 84.2441 < 2.2e-16 ***
## color 17038543 2 5.0848 0.006314 **
## carat 7435066381 1 4437.6815 < 2.2e-16 ***
## cut:color 7214868 2 2.1531 0.116534
## Residuals 2179746650 1301
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1broomExtra::glance(COVmodel)## Registered S3 method overwritten by 'broom.mixed':
## method from
## tidy.gamlss broom## # A tibble: 1 x 6
## logLik AIC BIC deviance nobs r.squared
## <dbl> <dbl> <dbl> <dbl> <int> <dbl>
## 1 -11225. 22467. 22508. 2179746650. 1308 0.774sjstats::anova_stats(car::Anova(COVmodel, type = 2)) %>% select(1:7)## term sumsq meansq df statistic p.value etasq
## cut cut 141145906 141145906 1 84.244 0.000 0.014
## color color 17038543 8519272 2 5.085 0.006 0.002
## carat carat 7435066381 7435066381 1 4437.681 0.000 0.760
## cut:color cut:color 7214868 3607434 2 2.153 0.117 0.001
## ...5 Residuals 2179746650 1675439 1301 NA NA NAWow that sure changed our results didn’t it? Suddenly cut and color matter!
Make no mistake they don’t have nearly the impact that carat does but at least
we can reliably see their impact on price by measures such as eta squared (etasq).
That’s because we originally had 9,553,303,035 in residual sums of squares but
by adding carat we’ve reduced that number to 2,308,863,799 which makes our
factors (cut and color) (the numerators) much more potent.
A quick peek into what’s changing may help. Let’s build a little tibble that
shows us what’s going on. The first three columns are straight from the
diamonds2 dataset, our price, cut, and color. The next column shows the
“prediction” made using our initial model. Every row with the same condition
e.g. “Fair” & “E” gets the same entry “3406” the mean for the cell. We can see
that when we use just carat as the predictor we get very different predictions
(although of course the same size gets the same prediction). Our COVmodel
predictions yield a third set of answers in the final column that makes use of
all the information available.
diamonds3 <- diamonds2 %>%
mutate(OriginalPred = predict(noCOVmodel),
WithCaratPred = predict(COVmodel),
CaratOnlyPred = predict(caratonly)) %>%
select(price, cut, color, OriginalPred, carat, CaratOnlyPred, WithCaratPred)
diamonds3## # A tibble: 1,308 x 7
## price cut color OriginalPred carat CaratOnlyPred WithCaratPred
## <int> <ord> <ord> <dbl> <dbl> <dbl> <dbl>
## 1 3407 Fair E 3406. 0.92 4193. 4094.
## 2 4844 Fair E 3406. 1.01 4828. 4743.
## 3 1098 Fair E 3406. 0.5 1230. 1065.
## 4 6221 Fair E 3406. 1.32 7015. 6978.
## 5 7918 Fair E 3406. 1 4757. 4671.
## 6 851 Fair E 3406. 0.5 1230. 1065.
## 7 814 Fair E 3406. 0.31 -111. -304.
## 8 1340 Fair E 3406. 0.51 1300. 1138.
## 9 1012 Fair E 3406. 0.34 101. -88.2
## 10 813 Fair E 3406. 0.4 524. 344.
## # … with 1,298 more rowsMore progress with emmeans
Okay, we’re making progress here but this isn’t all we can or should do. We have
a good sense that adding carat as a covariate makes for a much more accurate
model. But, we’re not interested in carat per se, it’s not that it’s
unimportant (clearly it matters) we’re just interested in what happens to cut
and color when we control for carat. That’s where the emmeans package can
help.
The emmeans package allows us to take our model(s) and compute the estimated
marginal means a.k.a. predicted model means or least squares means. The
package includes functions to not only compute them but also plot them as well
as make comparisons. We’ve already done that above for our model with no
covariate noCOVmodel but let’s see what that looks like just as a baseline.
# first the means
emmeans::pmmeans(noCOVmodel, "cut", by = "color")## color = E:
## cut pmmean SE df lower.CL upper.CL
## Fair 3406 184 1302 3045 3768
## Good 3425 184 1302 3063 3786
##
## color = F:
## cut pmmean SE df lower.CL upper.CL
## Fair 3392 184 1302 3031 3754
## Good 3196 184 1302 2835 3557
##
## color = G:
## cut pmmean SE df lower.CL upper.CL
## Fair 3340 184 1302 2979 3701
## Good 3517 184 1302 3156 3878
##
## Confidence level used: 0.95# then plot them
emmeans::emmip(noCOVmodel, cut ~ color, CIs = TRUE)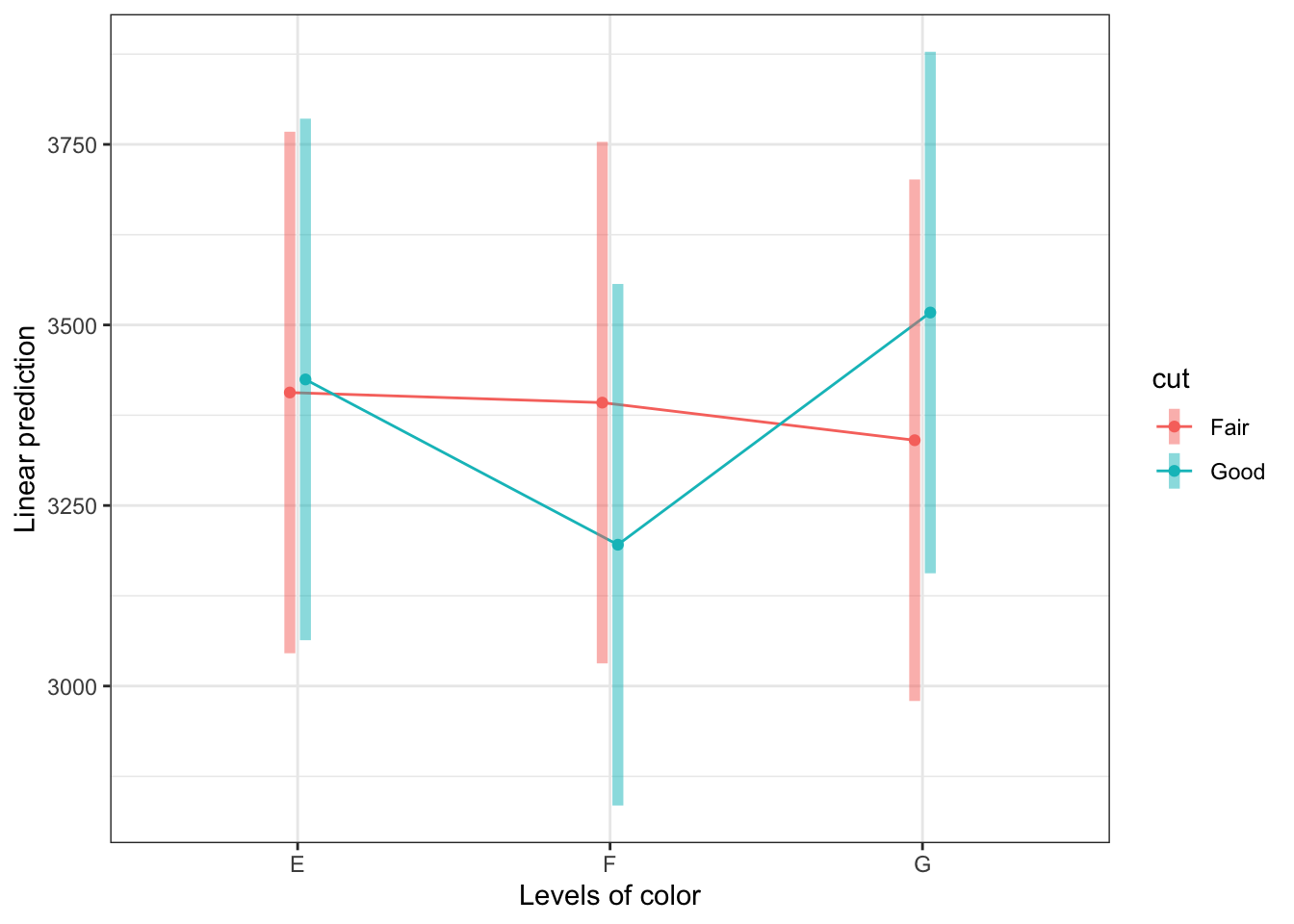
# pairwise comparisons
pairs(emmeans::pmmeans(noCOVmodel, "color", by = "cut"), adjust = "scheffe")## cut = Fair:
## contrast estimate SE df t.ratio p.value
## E - F 14.0 260 1302 0.054 0.9985
## E - G 66.1 260 1302 0.254 0.9683
## F - G 52.1 260 1302 0.200 0.9802
##
## cut = Good:
## contrast estimate SE df t.ratio p.value
## E - F 228.9 260 1302 0.879 0.6794
## E - G -92.6 260 1302 -0.356 0.9386
## F - G -321.5 260 1302 -1.235 0.4665
##
## P value adjustment: scheffe method with rank 2# not done above you can easily specify just one factor
emmeans::pmmeans(noCOVmodel, "cut")## NOTE: Results may be misleading due to involvement in interactions## cut pmmean SE df lower.CL upper.CL
## Fair 3380 106 1302 3171 3588
## Good 3379 106 1302 3171 3588
##
## Results are averaged over the levels of: color
## Confidence level used: 0.95# or the other factor
emmeans::pmmeans(noCOVmodel, "color")## NOTE: Results may be misleading due to involvement in interactions## color pmmean SE df lower.CL upper.CL
## E 3416 130 1302 3160 3671
## F 3294 130 1302 3039 3549
## G 3429 130 1302 3173 3684
##
## Results are averaged over the levels of: cut
## Confidence level used: 0.95Controlling for carat
None of that information is what we’re after however. We have the other model
COVmodel with carat added and what we need are the estimated means with
carat controlled for, or partialled out. We want to know the predicted or
estimated means for our 6 conditions as if size (carat) were controlled for.
emmeans::pmmeans(COVmodel, "carat")## carat pmmean SE df lower.CL upper.CL
## 0.805 3379 35.8 1301 3309 3450
##
## Results are averaged over the levels of: cut, color
## Confidence level used: 0.95emmeans::pmmeans(COVmodel, "cut", by = "color")## color = E:
## cut pmmean SE df lower.CL upper.CL
## Fair 3263 87.7 1301 3091 3435
## Good 3787 87.8 1301 3615 3959
##
## color = F:
## cut pmmean SE df lower.CL upper.CL
## Fair 3070 87.8 1301 2897 3242
## Good 3666 88.0 1301 3494 3839
##
## color = G:
## cut pmmean SE df lower.CL upper.CL
## Fair 2811 88.0 1301 2638 2984
## Good 3680 87.7 1301 3508 3852
##
## Confidence level used: 0.95emmip(COVmodel, cut ~ color, CIs = TRUE)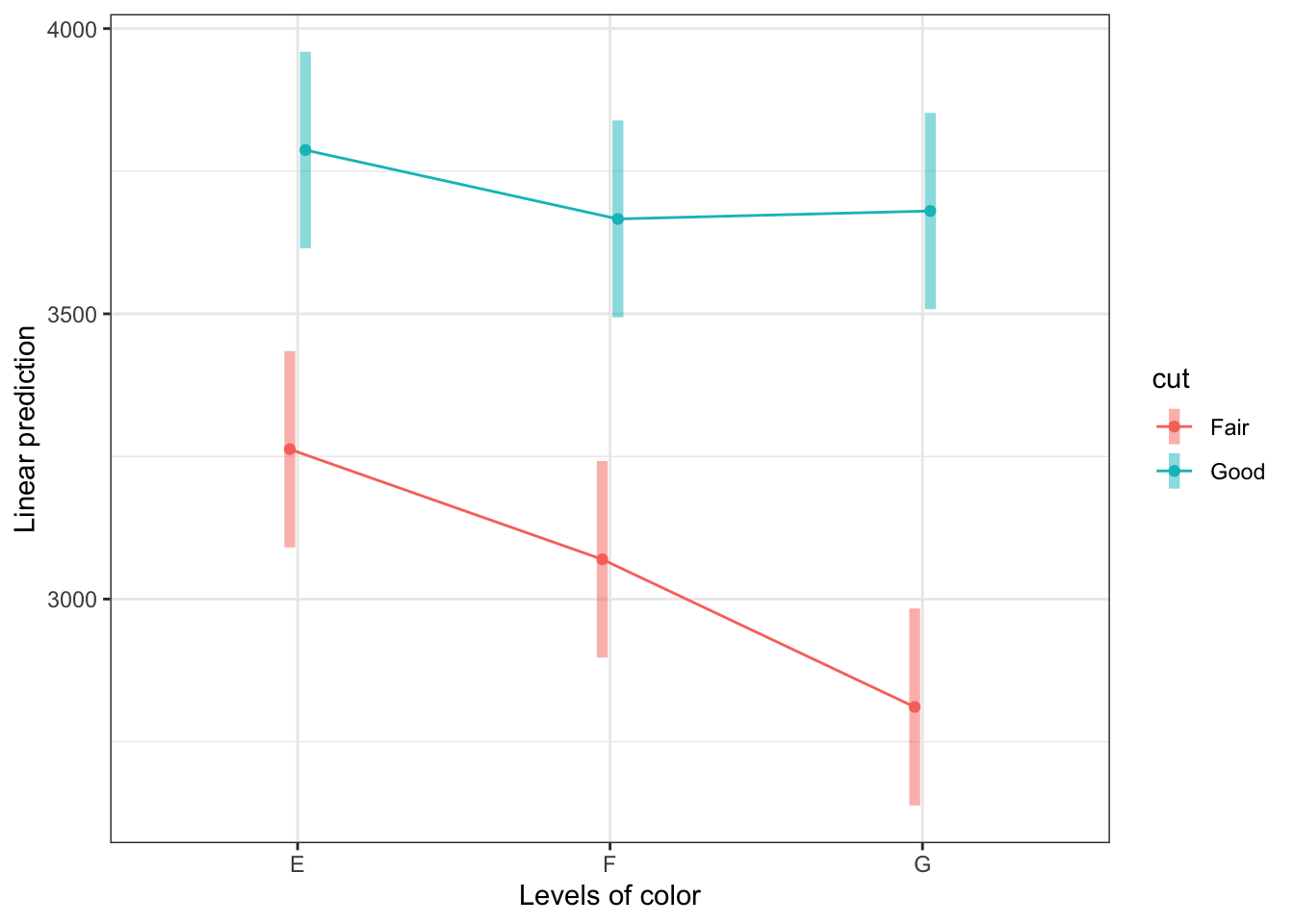
For me comparing the two plots tells a striking story about what role cut and
color play if we separate out the effect of size. If you look t the tables of
means you can see they are different but looking at the plot gives you a much
better idea of just how much the pattern has changed.
We can also run the appropriate significance tests using the very conservative
scheffe option.
pairs(emmeans::pmmeans(COVmodel, "cut", by = "color"), adjust = "scheffe")## color = E:
## contrast estimate SE df t.ratio p.value
## Fair - Good -524 124 1301 -4.222 <.0001
##
## color = F:
## contrast estimate SE df t.ratio p.value
## Fair - Good -597 125 1301 -4.791 <.0001
##
## color = G:
## contrast estimate SE df t.ratio p.value
## Fair - Good -869 124 1301 -6.988 <.0001pairs(emmeans::pmmeans(COVmodel, "color", by = "cut"), adjust = "scheffe")## cut = Fair:
## contrast estimate SE df t.ratio p.value
## E - F 193.0 124 1301 1.556 0.2984
## E - G 451.7 124 1301 3.640 0.0014
## F - G 258.8 124 1301 2.087 0.1138
##
## cut = Good:
## contrast estimate SE df t.ratio p.value
## E - F 120.7 124 1301 0.974 0.6226
## E - G 106.8 124 1301 0.861 0.6903
## F - G -13.9 124 1301 -0.112 0.9937
##
## P value adjustment: scheffe method with rank 2pairs(emmeans::pmmeans(COVmodel, "color"), adjust = "scheffe")## NOTE: Results may be misleading due to involvement in interactions## contrast estimate SE df t.ratio p.value
## E - F 157 87.7 1301 1.789 0.2022
## E - G 279 87.8 1301 3.182 0.0065
## F - G 122 87.8 1301 1.395 0.3781
##
## Results are averaged over the levels of: cut
## P value adjustment: scheffe method with rank 2pairs(emmeans::pmmeans(COVmodel, "cut"), adjust = "scheffe")## NOTE: Results may be misleading due to involvement in interactions## contrast estimate SE df t.ratio p.value
## Fair - Good -664 72.3 1301 -9.181 <.0001
##
## Results are averaged over the levels of: colorLet’s use ggplot to combine the two manually into one plot. We’ll plot the
original model with dashed lines and the new model with covariate in dark bold
lines.
withCOV <- broom::tidy(emmeans::pmmeans(COVmodel, "cut", by = "color"))
noCOV <- broom::tidy(emmeans::pmmeans(noCOVmodel, "cut", by = "color"))
ggplot(data = withCOV,
aes(x = color,
y = estimate,
group = cut,
color = cut)) +
geom_point(shape = 18,
size = 4) +
geom_line(size = 2) +
ggrepel::geom_label_repel(aes(label = round(estimate, 2)),
nudge_x = -.35,
color = "black") +
geom_point(data = noCOV,
aes(x = color,
y = estimate,
group = cut,
color = cut)) +
geom_line(data = noCOV,
aes(x =color,
y = estimate,
group = cut,
color = cut),
linetype = 2) +
ggrepel::geom_label_repel(data = noCOV,
aes(label = round(estimate, 2)),
nudge_x = .35,
color = "black") +
labs(title = "Estimated Mean Diamond Price",
subtitle = "Dashed line without carat as a covariate",
color = "Cut") +
ylab("Price") +
xlab("Color") +
expand_limits(y = c(2700,4200))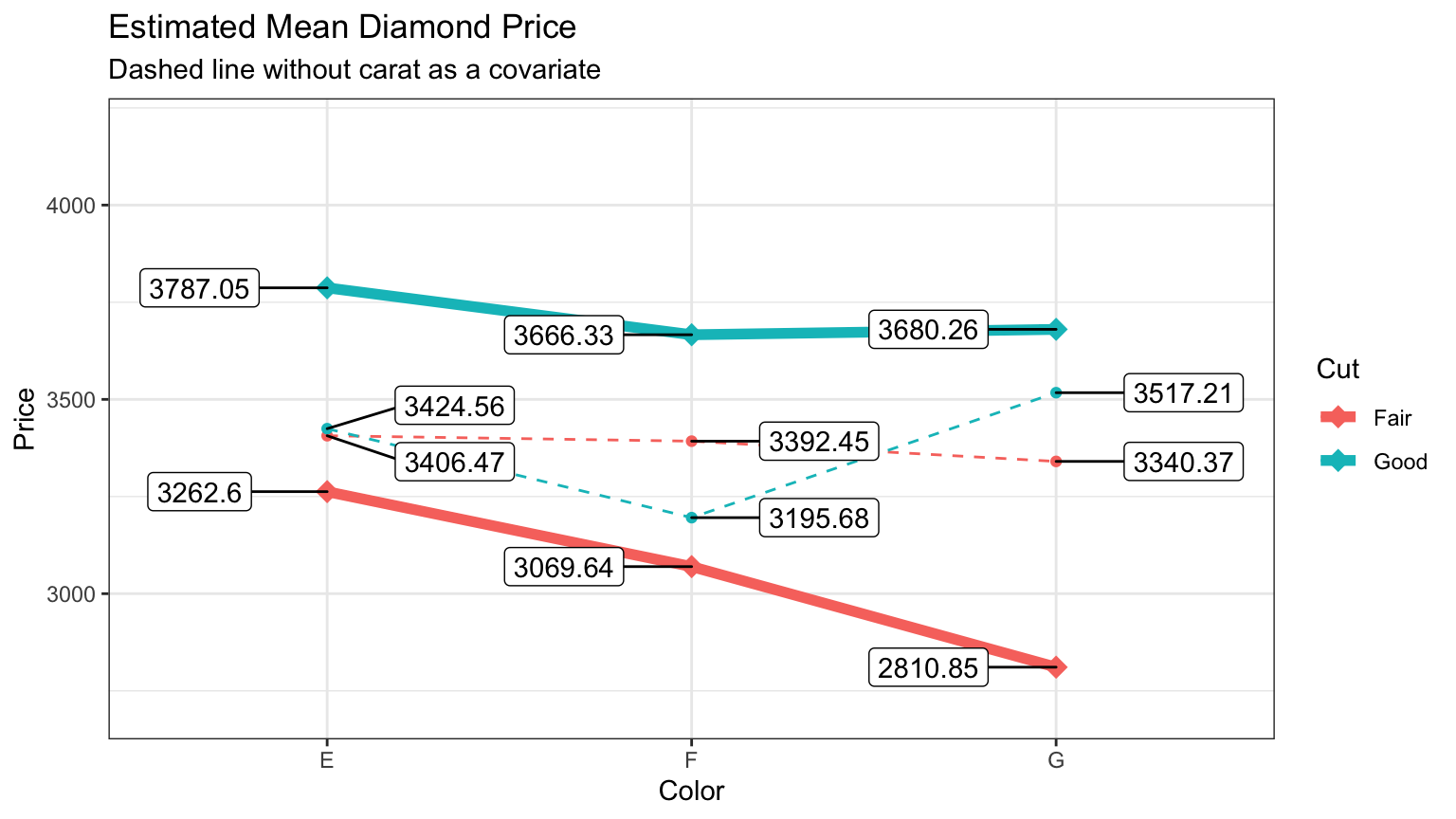
Measuring the effects
The final thing we’d like to do is to better our understanding of the “effect
size” of color and cut when we control for carat. Earlier we ran
sjstats::anova_stats(car::Anova(COVmodel, type = 2)) %>% select(1:7) but that
isn’t quite what we want, since the information about carat is still
influencing our computations. We want to remove carat from the calculations.
The trick to doing that in R with aov is to make carat an Error term. It
sounds strange in some ways if you ask me, but it is effective in getting what we
want.
Under the hood aov will create a model with two strata, Stratum 1 is all about
our covariate carat. It pulls out or controls for its influence so that Stratum
2 which is labelled “Within” now contains the ANOVA for the other variables
controlling for carat. The Within label always puts me off a bit since it
makes me want to think of a within subjects design (which this clearly isn’t).
But it’s having just the impact we like when you inspect the output. cut and
color do matter! There’s hope we’ll get published in the JODR yet.
COVmodelError <- aov(price ~ cut * color + Error(carat), diamonds2)
summary(COVmodelError)##
## Error: carat
## Df Sum Sq Mean Sq
## cut 1 7.283e+09 7.283e+09
##
## Error: Within
## Df Sum Sq Mean Sq F value Pr(>F)
## cut 1 1.405e+08 140501272 83.859 < 2e-16 ***
## color 2 1.704e+07 8519272 5.085 0.00631 **
## cut:color 2 7.215e+06 3607434 2.153 0.11653
## Residuals 1301 2.180e+09 1675439
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1car::Anova(COVmodelError$Within, type = 2)## Anova Table (Type II tests)
##
## Response: price
## Sum Sq Df F value Pr(>F)
## cut 141145906 1 84.2441 < 2.2e-16 ***
## color 17038543 2 5.0848 0.006314 **
## cut:color 7214868 2 2.1531 0.116534
## Residuals 2179746650 1301
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1broomExtra::glance(COVmodelError$Within)## NULLsjstats::anova_stats(car::Anova(COVmodelError$Within, type = 2)) %>% select(1:7)## term sumsq meansq df statistic p.value etasq
## cut cut 141145906 141145906 1 84.244 0.000 0.060
## color color 17038543 8519272 2 5.085 0.006 0.007
## cut:color cut:color 7214868 3607434 2 2.153 0.117 0.003
## ...4 Residuals 2179746650 1675439 1301 NA NA NAWhat don’t we know?
That this example would apply to across the rest of the dataset. Remember that one of the steps we took early on was to select only certain levels of our factors
colorandcutand even after that to choose balance over completeness.How badly we violated key assumptions about our data. We know we have some evidence of heteroskedasticity and non-normality. I also, for the sake of brevity, did not discuss interactions at the second order between the covariate and our factors.
Done!
I hope you’ve found this useful. I am always open to comments, corrections and suggestions.
Chuck (ibecav at gmail dot com)
